
科目:gzsx 来源:同步题 题型:单选题
科目:gzsx 来源: 题型:
4.下列命题正确的是( )
A.棱柱的底面一定是平行四边形
B.棱锥的底面一定是三角形
C.棱锥被平面分成的两部分不可能都是棱锥
D.棱柱被平面分成的两部分可以都是棱柱
科目:gzsx 来源:2009-2010学年北京市朝阳区高二(上)期中数学试卷(解析版) 题型:选择题
科目:gzsx 来源: 题型:单选题
科目:gzsx 来源: 题型:
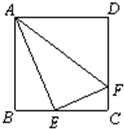 一个三棱柱恰好可放入一个正四棱柱的容体中,底面如图所示,其中三棱柱的底面AEF是一个直角三角形,∠AEF=90°,AE=a,EF=b,三棱柱的高与正四棱柱的高均为1,则此正四棱柱的体积为
一个三棱柱恰好可放入一个正四棱柱的容体中,底面如图所示,其中三棱柱的底面AEF是一个直角三角形,∠AEF=90°,AE=a,EF=b,三棱柱的高与正四棱柱的高均为1,则此正四棱柱的体积为科目:gzsx 来源: 题型:
 (2012•江门一模)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
(2012•江门一模)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.科目:gzsx 来源: 题型:
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
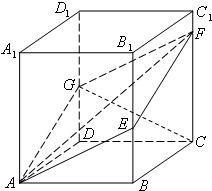 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,AA1⊥底面ABCD,AD=1,AB=2,∠BAD=60°,E、F分别是侧棱BB1、CC1上一点,BE=1,CF=2,平面AEF与侧棱DD1相交于G.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,AA1⊥底面ABCD,AD=1,AB=2,∠BAD=60°,E、F分别是侧棱BB1、CC1上一点,BE=1,CF=2,平面AEF与侧棱DD1相交于G.科目:gzsx 来源: 题型:
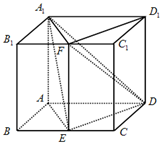 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.科目:gzsx 来源: 题型:
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.科目:gzsx 来源: 题型:
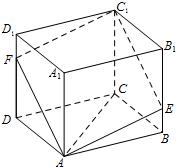 (2012•深圳二模)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,E,F分别在棱BB1,DD1上,且AF∥EC1.
(2012•深圳二模)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,E,F分别在棱BB1,DD1上,且AF∥EC1.| 6 |
科目:gzsx 来源:2011年哈尔滨三中、东北育才、大连育明、天津耀华四校高考数学二模试卷(文科)(解析版) 题型:解答题
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.科目:gzsx 来源:2010年广东省江门市高考数学二模试卷(理科)(解析版) 题型:解答题

科目:gzsx 来源:2010年广东省江门市高考数学模拟试卷(理科)(解析版) 题型:解答题

科目:gzsx 来源:2012年广东省江门市高考数学一模试卷(理科)(解析版) 题型:解答题

科目:gzsx 来源: 题型:解答题
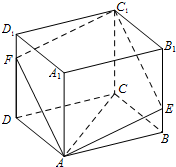 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,E,F分别在棱BB1,DD1上,且AF∥EC1.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,E,F分别在棱BB1,DD1上,且AF∥EC1. 的正方形,且BE=1,DF=2,求线段CC1的长,并证明:AC⊥EC1.
的正方形,且BE=1,DF=2,求线段CC1的长,并证明:AC⊥EC1.科目:gzsx 来源:2012年广东省深圳市高考数学二模试卷(文科)(解析版) 题型:解答题
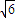 的正方形,且BE=1,DF=2,求线段CC1的长,并证明:AC⊥EC1.
的正方形,且BE=1,DF=2,求线段CC1的长,并证明:AC⊥EC1.
科目:gzsx 来源:2011-2012学年河南省新乡市卫辉一中高三(下)3月月考数学试卷(文科)(解析版) 题型:解答题
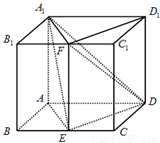 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.