科目：czsx 来源：江苏省泰州市海陵区2011-2012学年七年级上学期期末数学试题 题型：022
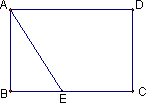
如图四边形AB
CD为长方形，从A到C有两条路线：第一条是从A→E→C；第二条是从A→D→C；其中较短的是第_______条．
科目：czsx 来源： 题型：
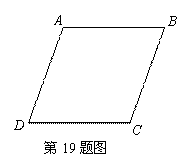
如图,四边形ABCD为菱形.
(1) 用直尺和圆规作出过菱形的顶点 A、B、C的圆，记为⊙O；
（要求保留作图痕迹，不必写出作法）
（2）连接OA，当∠D=70°时，求∠OAB的度数.
 |
科目：czsx 来源： 题型：
如图,四边形ABCD为边长等于4的菱形,
,点M为边AD上一点,点N为边DC上一点,
且AM=DN. (1)当AM=DN=3时,求
的面积.
（2）是否存在点M和点N，使的面积等于
？若存在，请指出点M和点N的位置；若不存在，请说明理由。
 |
科目：czsx 来源：鼎尖助学系列—同步练习(数学 九年级下册)、课题学习——中点四边形(1) 题型：044
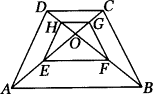
如图四边形ABCD为等腰梯形，AB∥CD，AD=BC，AC、BD相交于O，点E、F、G、H分别是AO、BO、CO、DO的中点．试判断四边形EFGH的形状，并说明理由．
科目：czsx 来源：数学教研室 题型：068
如图，ABCD为长方形的台球桌面，有白黑两球分别位于E、F点．
问：怎样撞击白球E，使白球先碰撞台边BC，反弹后再撞击台边DC，再反弹后击中黑球F．作出BC和CD的被击点的位置和白球的运动路线．(写出作图方法，保留作图痕迹)
科目：czsx 来源： 题型：
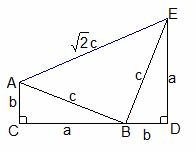
如图四边形ABCD是证明勾股定理时用到的一个图形，
、
、
是Rt△ABC和Rt△BDE的三边长，易知
.这时我们把形如
的方程称为关于
的 “勾系一元二次方程”.
请解决下列问题：
（1）构造一个“勾系一元二次方程”: .
（2）证明:关于的“勾系一元二次方程”必有实数根；
（3）若
是 “勾系一元二次方程”的一个根，且四边形
的周长是
，求△
的面积.
科目：czsx 来源： 题型：单选题
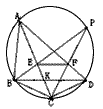
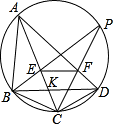如图四边形ABCD内接于圆，CB=CD．两个动点E﹑F各在AC﹑AD上，且满足EF∥BD，设BE交CF于点P，则点P的几何位置是科目：czsx 来源：广东省竞赛题 题型：单选题
科目：czsx 来源：2012-2013学年江苏省无锡市九年级下学期期中考试数学试卷（解析版） 题型：解答题
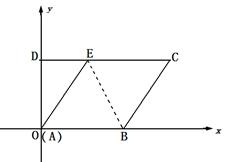
如图,四边形ABCD的边AB在X轴上，A与O重合，CD∥AB,D(0,
)，直线AE与CD交于E,DE=6。以BE为折痕，把点A翻恰好与点C重合；动点P从点D出发沿着D→C→B→O路径匀速运动，速度为每秒4个单位；以P为圆心的⊙P半径每秒增加
个单位，当点P在点D处时，⊙P半径为；直线AE沿y轴正方向向上平移，速度为每秒
个单位；直线AE、⊙P同时出发，当点P到终点O时两者都停止，运动时间为t;
(1) 求点B的坐标；
（2）求当直线AE与⊙P相切时t的值;
(3) 在整个运动过程中直线AE与⊙P相交的时间共有几秒？（直接写出答案）
科目：czsx 来源：2013届江苏省无锡市前洲中学九年级下学期期中考试数学试卷（带解析） 题型：解答题
如图,四边形ABCD的边AB在X轴上，A与O重合，CD∥AB,D(0,
)，直线AE与CD交于E,DE=6。以BE为折痕，把点A翻恰好与点C重合；动点P从点D出发沿着D→C→B→O路径匀速运动，速度为每秒4个单位；以P为圆心的⊙P半径每秒增加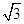
个单位，当点P在点D处时，⊙P半径为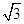；直线AE沿y轴正方向向上平移，速度为每秒
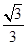个单位；直线AE、⊙P同时出发，当点P到终点O时两者都停止，运动时间为t;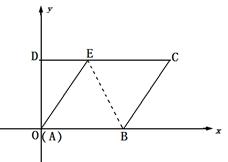
(1) 求点B的坐标；
（2）求当直线AE与⊙P相切时t的值;
(3) 在整个运动过程中直线AE与⊙P相交的时间共有几秒？（直接写出答案）
科目：czsx 来源：精编教材全解 数学 八年级上册 配苏科版 配苏科版 题型：044
某工厂的大门如图所示，其中四边形ABCD为长方形，上部是以AB为直径的半圆，其中AD＝2.3 m，AB＝2 m，现有一辆装满货物的大卡车，高2.5 m，宽1.6 m，试猜想这辆大卡车能否通过厂门？请说明理由．
CD为长方形，从A到C有两条路线：第一条是从A→E→C；第二条是从A→D→C；其中较短的是第 条；
15、如图，四边形ABCD为长方形，从A到C有两条路线：第一条是从A→E→C；第二条是从A→D→C；其中较短的是
，求EC的长。
上，点B在双曲线y
上，且AB∥x轴，C、D在x轴上，若四边形ABCD为长方形，则它的面积为（ ）。
如图，四边形ABCD是长方形的弹子球台面，有黑白两球分别位于M、N两点位置，试问：怎样撞击黑球M，才能使黑球碰撞台边AB反弹后击中白球N？