科目：gzsx 来源： 题型：
（08年宣武区质量检一文）（14分）
已知圆O:
和定点A（2，1），由圆O外一点P（a,b）向圆O引切线PQ，切点为Q，且满足
（1） 求实数a、b间满足的等量关系；
（2） 求线段PQ长的最小值；
（3） 若以P为圆心所做的圆P与圆Q有公共点，试求半径取最小值时，圆P的方程。
科目：gzsx 来源： 题型：
（08年宣武区质量检一文）（14分）
已知二次函数f(x)=
同时满足：
①不等式f(x)
0的解集有且只有一个元素②在定义域内存在0
,使得不等式
成立。设数列{
}的前n项和
.
（1） 求函数f(x)的表达式；
（2） 求数列{
}的通项公式；
设各项均不为零的数列{
}中，所有满足
的整数i的个数称为这个数列{
}的变号数。令
（n为正整数），求数列{}的变号数。
科目：gzsx 来源： 题型：
（08年宣武区质量检一文）（12分）
某车间准备从10名工人中选送4人到某生产线工作，工厂规定：这条生产线上熟练工人不得少于3人。已知这10名工人中熟练工人8名，学徒2名，
（1）求工人配置合理的概率；
（2）为了督促安全生产，工人安全部门每月对工人配置合理与否的情况进行三次检查，求其中两次检查得到结果是配置不合理的概率。
科目：gzsx 来源： 题型：
（08年宣武区质量检一文）定义：如果对于函数
定义与内的任意x, 都有
（M为常数），那么称M为的下界，下界M中的最大值叫做的下确界。现给出下列函数，其中所有有下确界的函数是 （ ）
①=cosx ②
③
④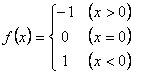
A. ① B. ④ C.②③④ D. ①③④
科目：gzsx 来源： 题型：
（08年宣武区质量检一）（14分）
根据定义在集合A上的函数y=
，构造一个数列发生器，其工作原理如下：
① 输入数据
，计算出
；
② 若
，则数列发生器结束工作；
若，则输出
，并将反馈回输入端，再计算出
。并依此规律继续下去。
现在有
，
。
（1） 求证：对任意，此数列发生器都可以产生一个无穷数列
；
（2） 若
，记
，求数列
的通项公式；
（3） 在（2）得条件下，证明
。
科目：gzsx 来源： 题型：
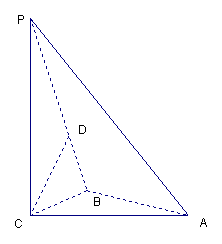
（08年宣武区质量检一）（13分）
如图，三棱锥P-ABC中，PC
平面ABC，PC=AC=2，
AB=BC，D是PB上一点，且CD平面PAB
（1） 求证：AB平面PCB；
（2） 求异面直线AP与BC所成角的大小；
（3） 求二面角C-PA-B 的大小的余弦值。
，点P在
，则此双曲线的离心率e的最大值是 
上有两点A、B，且AB垂直于y轴，若
，则抛物线的焦点到直线AB的距离是 （ ）
B、
C、
D、
，则它的体积是 
，向量a=(m,1), 若
,则m= （ ）
B. 
C. 
D. 
;
的距离;
展开式中，含
的项的系数是（ ）
的值为 （ ）
B.
C.
D.-
的反函数是 （ ）
B. 
D. 
，则实数a
的一条渐近线为y=2x，则双曲线的离心率e的值为 .