
科目:gzsx 来源: 题型:
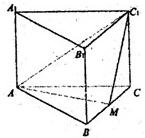 如图,正三棱柱ABC-A1B1C1的底面边长为a,点M在边BC上,△AMC1是以点M为直角顶点的等腰直角三角形.
如图,正三棱柱ABC-A1B1C1的底面边长为a,点M在边BC上,△AMC1是以点M为直角顶点的等腰直角三角形.科目:gzsx 来源:数学教研室 题型:044
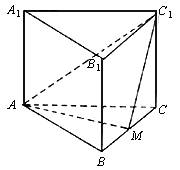
(1)求证:点M为边BC的中点;
(2)求点C到平面AMC1的距离;
(3)求二面角M-AC1-C的大小.
(乙)如图,直三棱柱ABC-A1B1C1中,底面是以ÐABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
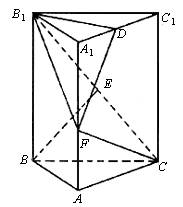
(1)求直线BE与A1C所成的角;
(2)在线段AA1上是否存在点F,使CF^平面B1DF,若存在,求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
科目:gzsx 来源:2010-2011学年重庆一中高二(下)月考数学试卷(文科)(解析版) 题型:解答题

科目:gzsx 来源: 题型:

(1)求证:点M为边BC的中点;
(2)求点C到平面AMC1的距离;
(3)求二面角M-AC1-C的大小.
科目:gzsx 来源:2006年高考第一轮复习数学:9.9 空间距离(解析版) 题型:解答题

科目:gzsx 来源: 题型:044
如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边BC上,△AMC1是以点M为直角顶点的等腰直角三角形.

(1)求证:点M为边BC的中点;
(2)求点C到平面AMC1的距离;
(3)求二面角M—AC1—C的大小.
科目:gzsx 来源: 题型:
(本小题满分12分)
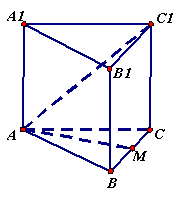 如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边 BC上,△AMC1是以点M为直角顶点的等腰直角三角形。
如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边 BC上,△AMC1是以点M为直角顶点的等腰直角三角形。
(Ⅰ)求证点M为边BC的中点;
(Ⅱ)求点C到平面AMC1的距离;
(Ⅲ)求二面角M—AC1—C的大小。
科目:gzsx 来源:2007年天津市汉沽一中高三第一次调研数学试卷(解析版) 题型:解答题

科目:gzsx 来源:2010年吉林省长春五中高考数学三模试卷(理科)(解析版) 题型:解答题

科目:gzsx 来源:2010年新教材高考数学模拟题详解精编试卷(6)(解析版) 题型:解答题
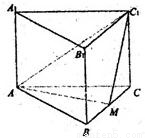
科目:gzsx 来源:2012年山东省聊城市冠县武训高中高考数学模拟试卷(理科)(解析版) 题型:解答题
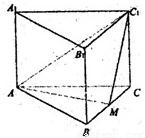
科目:gzsx 来源:数学教研室 题型:044

(1)求证:点M为边BC的中点;
(2)求点C到平面AMC1的距离;
(3)求二面角M—AC1—C的大小.
科目:gzsx 来源: 题型:044
(甲)如图,正三棱柱ABC-A1B1C1的底面边长为a,点M在边BC上,DAMC1是以点M为直角顶点的等腰直角三角形.

(1)求证:点M为边BC的中点;
(2)求点C到平面AMC1的距离;
(3)求二面角M-AC1-C的大小.
(乙)如图,直三棱柱ABC-A1B1C1中,底面是以ÐABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.

(1)求直线BE与A1C所成的角;
(2)在线段AA1上是否存在点F,使CF^平面B1DF,若存在,求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
科目:gzsx 来源: 题型:
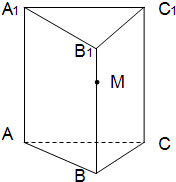 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,点M在侧棱BB1上.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,点M在侧棱BB1上.| 2 |
科目:gzsx 来源:0103 期末题 题型:解答题
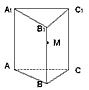
 ,求异面直线AM与BC所成的角;
,求异面直线AM与BC所成的角;科目:gzsx 来源:2008-2009学年河北省唐山一中高二(下)期末调研数学试卷(解析版) 题型:解答题
 ,求异面直线AM与BC所成的角;
,求异面直线AM与BC所成的角;
科目:gzsx 来源: 题型:
 如图,正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>3),点M在侧棱BB1上移动,并且M到底面ABC的距离为x,且AM与侧面BCC1B1所成的角为α.
如图,正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>3),点M在侧棱BB1上移动,并且M到底面ABC的距离为x,且AM与侧面BCC1B1所成的角为α.| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
科目:gzsx 来源:2007-2008学年黑龙江省哈尔滨六中高二(下)期中数学试卷(文科)(解析版) 题型:解答题
 上变化,求x的变化范围;
上变化,求x的变化范围;  ,求AM与BC所成角的余弦值.
,求AM与BC所成角的余弦值.
科目:gzsx 来源: 题型:
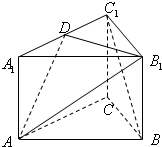 如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
| ||
| 2 |
科目:gzsx 来源: 题型:
 如图,正三棱柱ABC-A1B1C1的底面边长为8,对角线B1C=10,D为AC的中点.
如图,正三棱柱ABC-A1B1C1的底面边长为8,对角线B1C=10,D为AC的中点.