科目：gzsx 来源： 题型：
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 6 |
| π |
| 3 |
| 399 |
| 2 |
科目：gzsx 来源：不详 题型：填空题
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 6 |
| π |
| 3 |
| 399 |
| 2 |
科目：gzsx 来源： 题型：
已知
，
，
（Ⅰ）若f(x)在
处取得极值，试求c的值和f(x)的单调增区间；
（Ⅱ）如图所示：若函数
的图象在
连续光滑，试猜想拉格朗日中值定理：即一定存在
使得
，利用这条性质证明：函数y=g(x)图象上任意两点的连线斜率不小于2e－4。
科目：gzsx 来源：2010-2011学年浙江省杭州市高二上学期开学考试数学卷 题型：解答题
(本小题满分10分)
已知
（Ⅰ）若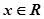
，求f(x)的单调增区间；
（Ⅱ）若
时，f(x)的最大值为4，求a的值.
科目：gzsx 来源： 题型：
已知
，
，
（Ⅰ）若f(x)在
处取得极值，试求c的值和f(x)的单调增区间；
（Ⅱ）如图所示：若函数
的图象在
连续光滑，试猜想拉格朗日中值定理：即一定存在
使得
，利用这条性质证明：函数y=g(x)图象上任意两点的连线斜率不小于2e－4。
科目：gzsx 来源： 题型：
（本题满分14分）已知
，
，
（1）若f(x)在
处取得极值，试求c的值和f(x)的单调增区间；
（2）如右图所示，若函数
的图象在
连续光滑，试猜想拉格朗日中值定理：即一定存在
使得
？（用含有a,b,f(a),f(b)的表达式直接回答）
（3）利用（2）证明：函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
科目：gzsx 来源：浙江省东阳市南马高中2010届高三上学期期中考试数学文科试题 题型：044
已知函数f(x)＝asin2x＋bcos2x＋2的图象经过点(0，3)和(
，4)．
(Ⅰ)求函数f(x)的单调增区间；
(Ⅱ)已知f(α)＝3，且α∈
，求α的值．
科目：gzsx 来源：湖南省长郡中学2012届高三第五次月考数学文科试题 题型：044
已知向量
＝(sinx，1)，
＝(
cosx，
)，函数f(x)＝(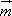
＋
)·
．
(1)求函数f(x)的单调增区间；
(2)在△ABC中，内角A，B，C所对的边分别为a，b，c，A为锐角，a＝2
，c＝4且f(A)是函数f(x)在[0，
]上的最大值，求△ABC的面积S．
科目：gzsx 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044
已知f(x)＝2cos2x＋
sin2x＋a(a∈R)
①若x∈R，求f(x)的单调增区间
②若x∈[0，
]时，f(x)的最大值为4，求a的值．
③(理)在②的条件下，求满足f(x)＝1且x∈[－π，π]的x的集合．
科目：gzsx 来源：模拟题 题型：解答题
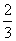x3-2x2+cx+4，g(x)=ex-e2-x+f(x)，
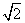处取得极值，试求c的值和f(x)的单调增区间；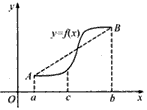
科目：gzsx 来源：辽宁省沈阳二中2008－2009学年高三上学期期中考试(数学文) 题型：044
已知函数f(x)＝mx3－3(m＋1)x2＋(3x＋6)x＋1，其中m＜0．
(1)若f(x)的单调增区间是(0，1)求m的值．
(2)当x∈[－1，1]时，函数y＝f(x)的图象上任意一点的切线斜率恒大于3m，求m的取值范围．
科目：gzsx 来源：高中数学全解题库(国标苏教版·必修4、必修5) 苏教版 题型：044
已知函数
(1)求当a＝1时f(x)的单调增区间：
(2)当a＜0且x∈[0，π]时，f(x)的值域为[3，4]，求a，b的值．
科目：gzsx 来源：北京市东城区2000～2001学年度第一学期期末抽测试卷高一数学 题型：044
已知函数f(x)=
x＋2sinxcosx＋3
x，x∈R．
(1)求f(x)的最小正周期．
(2)求f(x)的单调增区间．
(3)求f(x)的最小值，并求f(x)取得是小值时自变量x的集合．
科目：gzsx 来源： 题型：
| α |
| 2 |
| π |
| 2 |
科目：gzsx 来源： 题型：
(本小题满分12分) 已知定义在R上的函数f(x)=
的周期为
，
且对一切x
R，都有f(x)
；
（1）求函数f(x)的表达式；
（2）若g(x)=f(
),求函数g(x)的单调增区间；
(3) 若函数y=f(x)－3的图象按向量
=(m，n) (|m|<
)平移后得到一个奇函数的图象，求实数m、n的值.
科目：gzsx 来源： 题型：
(1)求函数f(x)的最大值及取得最大值的自变量x的集合;
(2)函数f(x)的单调增区间.
科目：gzsx 来源：辽宁省2012届高二下学期期末考试数学（文） 题型：解答题
(本小题满分12分)已知f(x)=ex-ax-1.
（1）求f(x)的单调增区间；
（2）若f(x）在定义域R内单调递增，求a的取值范围；
（3）是否存在a,使f(x)在（-∞，0］上单调递减，在［0，+∞）上单调递增？若存在，求出a的值；若不存在，说明理由.
科目：gzsx 来源：2010-2011学年山东省高三第二次质量检测文科数学卷 题型：解答题
已知a是实数，函数f(x)＝x2(x－a)
(1)若f′(1)＝3，求a的值及曲线y＝f(x)在点(1，f(1))处的切线方程；
(2)a>0,求f(x)的单调增区间．
，求f(x)的单调增区间；
时，f(x)的最大值为4，求a的值；
的x的集合。
x＋
),求函数在
的单调增区间（2）计算：