科目：czsx 来源： 题型：

23、如图，MN⊥CD于G，MN⊥AB于H，直线EF分别交AB、CD于G、Q，且∠GQC=120°，求∠EGB的度数．

科目：czsx 来源： 题型：解答题

科目：czsx 来源：中学学习一本通　数学　七年级下册 北师大课标 题型：022

如图，OE⊥CD于O，直线AB，CD交于O，那么，∠AOD的补角有________和________，∠AOE的余角有________，∠DOF的补角有________，图中的对顶角是________

科目：czsx 来源： 题型：

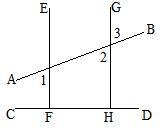22、在以下证明中的括号内注明理由：
已知：如图，EF⊥CD于F，GH⊥CD于H．
求证：∠1=∠3．
证明：∵EF⊥CD，GH⊥CD（已知），
∴EF∥GH（

垂直于同一条直线的两直线平行

）．
∴∠1=∠2（

两直线平行，同位角相等

）．
∵∠2=∠3（

对顶角相等

），
∴∠1=∠3（

等量代换

）．

科目：czsx 来源：2014届安徽凤阳三中七年级下期末数学试卷（解析版） 题型：解答题

补充填空：如图，BE⊥CD于E，AF⊥CD于F，∠1=∠2，说明AC∥BD的理由。

 

 

科目：czsx 来源：不详 题型：解答题

在以下证明中的括号内注明理由：
已知：如图，EF⊥CD于F，GH⊥CD于H．
求证：∠1=∠3．
证明：∵EF⊥CD，GH⊥CD（已知），
∴EF∥GH（______）．
∴∠1=∠2（______）．
∵∠2=∠3（______），
∴∠1=∠3（______）．

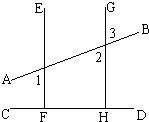
科目：czsx 来源：2012-2013学年北京市顺义一中八年级（上）入学数学测试卷（解析版） 题型：解答题

在以下证明中的括号内注明理由：
已知：如图，EF⊥CD于F，GH⊥CD于H．
求证：∠1=∠3．
证明：∵EF⊥CD，GH⊥CD（已知），
∴EF∥GH（______）．
∴∠1=∠2（______）．
∵∠2=∠3（______），
∴∠1=∠3（______）．

科目：czsx 来源： 题型：填空题

科目：czsx 来源： 题型：

如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，么∠A=42°，求∠D的度数．

科目：czsx 来源： 题型：

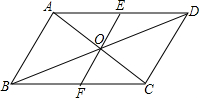如图，AB∥CD，AD∥BC，过O任作直线EF，交AD于E，交BC于F．
（1）图中有

6

6

对全等三角形；
（2）要证明OE=OF，只要证明△

AOE

AOE

≌△

COF

COF

或△

DOE

DOE

≌△

BOF

BOF

．

科目：czsx 来源： 题型：

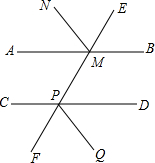如图，AB∥CD，直线EF分别交AB、CD于从P，MN、PQ分别平分∠AME和∠DPF，
（1）试说明：∠AMN=∠DPQ；
（2）试说明：MN∥PQ．

科目：czsx 来源： 题型：

按要求画图（要用铅笔和直尺画图并保留画图痕迹）
（1）如图，平面内的线段AB，BC，CD，DA首尾相接，按照下列要求画图：
①连接AC，BD相交于点O；
②分别延长线段AD，BC相交于点P；
③分别延长线段BA，CD相交于点Q．
（2）如图，AB表示一条公路，公路两旁分别有一个工厂M和N．要在公路旁建一个货场，使它到M，N两点距离之和最小，货场应建在哪里？在图上画出表示货场位置的点．保留画图痕迹，并回答下列问题：你画图得到点P的依据是

两点之间线段最短

两点之间线段最短

．

科目：czsx 来源： 题型：

22、如图，AB是⊙O的直径，AE平分∠BAF交⊙O于点E，过点E作直线与AF垂直交AF延长线交于D点，且交AB延长线于C点．说明：CD与⊙O相切于点E．

科目：czsx 来源： 题型：

已知：如图，AB∥CD，EF交AB于G，交CD于F，FH平分∠EFD，∠EFD=100°．求：∠AHF，∠AGE的度数．

科目：czsx 来源： 题型：

如图，AB∥CD，直线EF分别交AB、CD于点E、F，∠CFE=112°，EG平分∠BEF，交CD于点G，则∠EGF=

56

56

 度．

科目：czsx 来源： 题型：

如图，AB是⊙O的直径，CD切⊙O于点C，BE⊥CD于E，连接AC、BC．
（1）求证：BC平分∠ABE；
（2）若⊙O的半径为2，∠A=60°，求CE的长．

科目：czsx 来源： 题型：

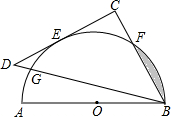（2013•宁波模拟）如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．
（1）求量角器在点G处的读数α（0°＜α＜90°）；
（2）若AB=10cm，求阴影部分面积．

科目：czsx 来源： 题型：

如图，AB⊙O的直径，CD⊥AB于E，连OC，OC=5，CD=8，则tan∠COE=

4

3

4

3

．

科目：czsx 来源： 题型：

如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E、F为圆心，大于

1

2

EF的长为半径画弧，两弧交于点P，作射线AP，交CD于点M．若∠ACD=120°，则∠MAB的度数为

 

．

科目：czsx 来源： 题型：

如图，AB是⊙O的直径，D是弦BC延长线上一点，DE⊥AB于点E，交AC于点H，F在ED上，且FC=FD．
（1）求证：CF是⊙O的切线；
（2）若FD=1，∠D=30°，AC=CD，求AH的长．