三角形ABC中AD为角平分线 AB=10AC=8 角ABC面积为45答案解析
科目:czsx
来源:中华题王 数学 八年级上 (人教版) 人教版
题型:047
查看答案和解析>>
科目:czsx
来源:
题型:
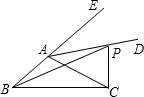
如图所示,在△ABC中,AD为外角平分线,P为AD上任意一点,AB+AC和BP+PC有什么关系.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
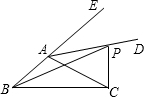 如图所示,在△ABC中,AD为外角平分线,P为AD上任意一点,AB+AC和BP+PC有什么关系.
如图所示,在△ABC中,AD为外角平分线,P为AD上任意一点,AB+AC和BP+PC有什么关系.
查看答案和解析>>
科目:czsx
来源:
题型:047
如图,∠CAE是△ABC的一个外角,AD为其平分线,若AD//BC,求证:AB=AC.

查看答案和解析>>
科目:czsx
来源:
题型:047
如图,∠CAE是△ABC的一个外角,AD为其平分线,若AD//BC,求证:AB=AC.

查看答案和解析>>
科目:czsx
来源:
题型:
在直角三角形ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB的角平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( )
查看答案和解析>>
科目:czsx
来源:
题型:044
如图,在△ABC中,∠B=90°,AD为角平分线,DE⊥AC,∠C=30°,则图中有等腰三角形多少个,并指出来.

查看答案和解析>>
科目:czsx
来源:设计八年级上数学人教版 人教版
题型:047
角平分线与三角形面积,有下列正确命题成立:在△ABC中,
(1)若AD为角平分线,则S△ABD∶S△ACD=AB∶AC;
(2)设D为BC上一点,连结AD,若S△ABD∶S△ACD=AB∶AC,则AD为角平分线.

查看答案和解析>>
科目:czsx
来源:数学教研室
题型:044
如图,在△ABC中,∠B=90°,AD为角平分线,DE⊥AC,∠C=30°,则图中有等腰三角形多少个,并指出来.

查看答案和解析>>
科目:czsx
来源:
题型:填空题
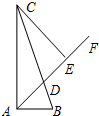
【阅读理解】
已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.求证:AC=AB+BD证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
【解决问题】
已知,如图2,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的平分线,交BC边于点D,DE⊥AC,垂足为E,若AB=2,则三角形DEC的周长为________.
【数学思考】:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D如图3”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
【类比猜想】
任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图4,请你写出线段AC、AB、BD之间的数量关系.
查看答案和解析>>
科目:czsx
来源:
题型:单选题
 在直角三角形ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB的角平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为
在直角三角形ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB的角平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为
- A.
63°
- B.
45°
- C.
27°
- D.
18°
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•黄石)如图1所示:等边△ABC中,线段AD为其内角角平分线,过D点的直线B
1C
1⊥AC于C
1交AB的延长线于B
1.
(1)请你探究:
=,
=是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问
=一定成立吗?并证明你的判断.
(3)如图2所示Rt△ABC中,∠ACB=90︒,AC=8,AB=
,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求
的值.
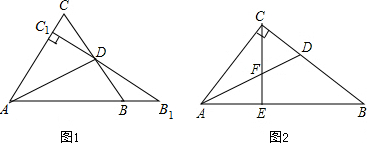
查看答案和解析>>
科目:czsx
来源:
题型:
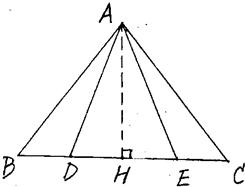
29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.
解:过点A作AH⊥BC,垂足为H.
∵在△ADE中,AD=AE(已知)
AH⊥BC(所作)
∴DH=EH(等腰三角形底边上的高也是底边上的中线)
又∵BD=CE(已知)
∴BD+DH=CE+EH(等式的性质)
即:BH=
CH
又∵
AH⊥BC
(所作)
∴AH为线段
BC
的垂直平分线
∴AB=AC(线段垂直平分线上的点到线段两个端点的距离相等)
∴
∠B=∠C
(等边对等角)
查看答案和解析>>
科目:czsx
来源:
题型:
(1)在如图的正方形中,以右上角顶点为旋转中心,按逆时针旋转一定角度后使之与原图形成轴对称,其中对称轴是原图形的某条边,并指出这时旋转角为多少度.
(2)在平行四边形ABCD中,∠BCD的平分线CE交AD于E,∠ABC的平分线BG

交CE于F,交AD于G.试说明:AE=DG.
查看答案和解析>>
科目:czsx
来源:
题型:
直角三角形ABC中两锐角的平分线AD、BE的交点为P,则∠APB的度数为( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在等腰△ABC中,∠C=90°,AD为角平分线,过D作斜边AB的垂线,交AB于点E.若AB=8cm,则△DEB的周长为
cm.
查看答案和解析>>
科目:czsx
来源:
题型:

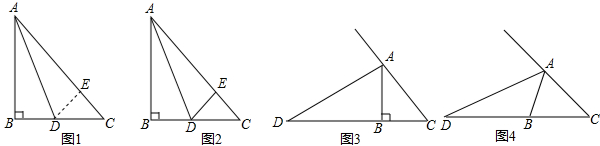
18、已知Rt△ABC中,∠B=90°.
(1)根据要求作图(尺规作图,保留作图痕迹,不写画法).
①作∠BAC的平分线AD交BC于D;
②作线段AD的垂直平分线交AB于E,交AC于F,垂足为H;
③连接ED.
(2)在(1)的基础上写出一对相似比不为1的相似三角形和一对全等三角形:
△
AHF
∽△
ABD
;△
AHF
≌△
AHE
.
并选择其中一对加以证明.
查看答案和解析>>
科目:czsx
来源:
题型:
△ABC中,∠C=90°,AD为角平分线,BC=32,BD:DC=5:3,则点D到AB的距离为( )
查看答案和解析>>
科目:czsx
来源:
题型:

5、已知Rt△ABC中,∠B=90°
(1)根据要求作图(尺规作图,保留作图痕迹,不写画法)
①作∠BAC的平分线AD交BC于D;
②作线段AD的垂直平分线交AB于E,交AC于F,垂足为H;
③连接ED.
(2)在(1)的基础上写出一对相似比不为1的相似三角形和一对全等三角形:
△AHF∽△ACD,△AHE∽△ACD,△DHE∽△ACD,△BDE∽△BCA等
;
全等三角形有△AHF≌△AHE,△ACD≌△AHE,△AHF≌△DHE
.
回顾体会联想
.
查看答案和解析>>
科目:czsx
来源:
题型:
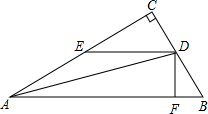
如图,Rt△ABC中,∠CAB=30°,AD为角平分线,DE∥AB,DF⊥AB于F,若AE=8cm,则DF的长为
4cm
4cm
cm.
查看答案和解析>>

![]() =
=![]()
![]() =
=![]() ,求证:AD为角平分线.
,求证:AD为角平分线.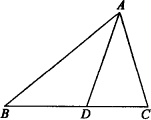
 在直角三角形ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB的角平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( )
在直角三角形ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB的角平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( )

 在直角三角形ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB的角平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为
在直角三角形ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB的角平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为
 29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.
29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据. 交CE于F,交AD于G.试说明:AE=DG.
交CE于F,交AD于G.试说明:AE=DG. 18、已知Rt△ABC中,∠B=90°.
18、已知Rt△ABC中,∠B=90°. 5、已知Rt△ABC中,∠B=90°
5、已知Rt△ABC中,∠B=90°