
科目:czsx 来源: 题型:
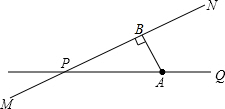 如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,点A到公路MN的距离为80m,现有一拖拉机在公路MN上以18km/h的速度沿PN方向行驶,拖拉机行驶时周围100m以内都会受到噪音声的影响,试问该校受影响的时间为多少秒?
如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,点A到公路MN的距离为80m,现有一拖拉机在公路MN上以18km/h的速度沿PN方向行驶,拖拉机行驶时周围100m以内都会受到噪音声的影响,试问该校受影响的时间为多少秒?科目:czsx 来源: 题型:解答题
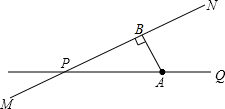 如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,点A到公路MN的距离为80m,现有一拖拉机在公路MN上以18km/h的速度沿PN方向行驶,拖拉机行驶时周围100m以内都会受到噪音声的影响,试问该校受影响的时间为多少秒?
如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,点A到公路MN的距离为80m,现有一拖拉机在公路MN上以18km/h的速度沿PN方向行驶,拖拉机行驶时周围100m以内都会受到噪音声的影响,试问该校受影响的时间为多少秒?科目:czsx 来源: 题型:
| 2 |
| x |
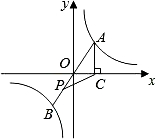 是线段OB上的动点,连接CP,设△ACP的面积为S,则下列说法正确的是( )
是线段OB上的动点,连接CP,设△ACP的面积为S,则下列说法正确的是( )| A、S>1 | B、S>2 |
| C、1<S<2 | D、1≤S≤2 |
科目:czsx 来源:1998年浙江省湖州市中考数学试卷 题型:填空题
科目:czsx 来源:2006年中考数学模拟试题 题型:059
解答题
阅读下列材料并填空.平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
(1)分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
(2)归纳:考察点的个数和可连成直线的条数![]() 发现:如下表
发现:如下表

(3)推理:平面上有n个点,两点确定一条直线.取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即![]()
(3)结论:![]()
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出________个三角形;
当仅有4个点时,可作出________个三角形;
当仅有5个点时,可作出________个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数![]() ,发现:(填下表)
,发现:(填下表)

(3)推理:________
(4)结论:________
科目:czsx 来源:湖州 题型:填空题
科目:czsx 来源:2010年新疆维吾尔自治区新疆生产建设兵团年初中学业水平考试 题型:044
如图是一个量角器和一个含30°角的直角三角形放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OE

(1)求证:DE∥CF;
(2)当OE=2时,若以O、B、F为顶点的三角形与△ABC相似,求OB的长
(3)若OE=2,移动三角板ABC且使AB边始终与半圆O相切,直角顶点B在直径DE的延长线上移动,求出点B移动的最大距离
科目:czsx 来源: 题型:044
阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
(1
)分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……(2
)归纳:考察点的个数和可连成直线的条数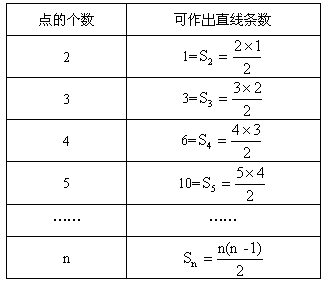
(3)
推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即(4
)结论:试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1
)分析:当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2
)归纳:考察点的个数n和可作出的三角形的个数|
点的个数 |
可连成三角形个数 |
|
3 |
|
|
4 |
|
|
5 |
|
|
…… |
|
|
n |
(3)
推理: (4)结论:科目:czsx 来源:1998年全国中考数学试题汇编《圆》(02)(解析版) 题型:填空题
科目:czsx 来源: 题型:填空题
科目:czsx 来源:专项题 题型:填空题
 有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7
有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7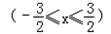 与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大,则点M为_________.
与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大,则点M为_________.科目:czsx 来源:专项题 题型:填空题
 有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7
有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7 与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大,则点M为( )
与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大,则点M为( )科目:czsx 来源:专项题 题型:填空题
 有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7
有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7 与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大,则点M为_________.
与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大,则点M为_________.科目:czsx 来源:专项题 题型:填空题
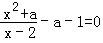 有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7
有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7 与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大,则点M为( )。
与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大,则点M为( )。科目:czsx 来源: 题型:
| x2+a |
| x-2 |
| 3 |
| 2 |
| 3 |
| 2 |
科目:czsx 来源:2007年安徽省蚌埠二中自主招生考试数学素质测试卷(解析版) 题型:解答题
 有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7
有一个增根为b,另一根为c.二次函数y=ax2+bx+c+7 与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大.
与x轴交于P和Q两点.在此二次函数的图象上求一点M,使得△PQM面积最大.科目:czsx 来源:2012年苏教版初中数学七年级上1.1生活数学练习卷(解析版) 题型:填空题
将一根绳子两端分别涂上红色和白色,再在中间随意画3个圆点, 涂上白色或红色,然后在这三个圆点处把绳子剪断,这样所得到的各小段两端都有颜色.则两端颜色不同的小段数目一定是________(答奇数或偶数)_________________.
科目:czsx 来源:2010年云南省玉溪市中考数学试题 题型:059
如图,在平面直角坐标系中,点A的坐标为(1,![]() ),△AOB的面积是
),△AOB的面积是![]() .
.
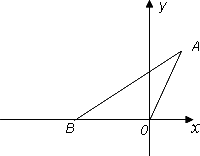
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(4)在(2)中x轴下方的抛物线上是否存在一点P,过点P作x轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2∶3?若存在,求出点P的坐标;若不存在,请说明理由.