
科目:czsx 来源: 题型:
 28、在等腰直角△ABC中,∠C=90°,AC=BC,D是AB上任一点,AE⊥CD于E,BF⊥CD交CD延长线于F,CH⊥AB于H,交AE于G.求证:(1)BD=CG;(2)DF=GE.
28、在等腰直角△ABC中,∠C=90°,AC=BC,D是AB上任一点,AE⊥CD于E,BF⊥CD交CD延长线于F,CH⊥AB于H,交AE于G.求证:(1)BD=CG;(2)DF=GE.科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:解答题
 在等腰直角△ABC中,∠C=90°,AC=BC,D是AB上任一点,AE⊥CD于E,BF⊥CD交CD延长线于F,CH⊥AB于H,交AE于G.求证:(1)BD=CG;(2)DF=GE.
在等腰直角△ABC中,∠C=90°,AC=BC,D是AB上任一点,AE⊥CD于E,BF⊥CD交CD延长线于F,CH⊥AB于H,交AE于G.求证:(1)BD=CG;(2)DF=GE.科目:czsx 来源: 题型:
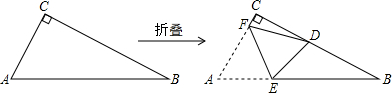
科目:czsx 来源: 题型:
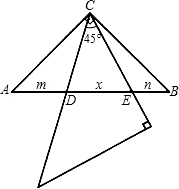 点D不与点A重合,点E不与点B重合),设AD=m,DE=x,BE=n.
点D不与点A重合,点E不与点B重合),设AD=m,DE=x,BE=n.科目:czsx 来源: 题型:
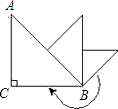 如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰直角三角形,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边重叠为止,此时这个三角形的斜边长为
如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰直角三角形,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边重叠为止,此时这个三角形的斜边长为科目:czsx 来源: 题型:
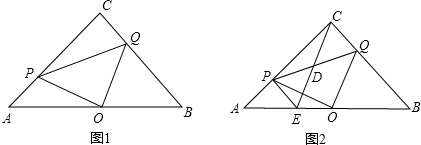
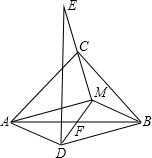 如图,等腰直角三角形ABC中,∠ACB=90°,AC=BC,M是△ABC内任意一点,连结MC并延长到E,使得CE=CM,以MA、MB为邻边做▱MADB,对角线交点为F,连接DE.
如图,等腰直角三角形ABC中,∠ACB=90°,AC=BC,M是△ABC内任意一点,连结MC并延长到E,使得CE=CM,以MA、MB为邻边做▱MADB,对角线交点为F,连接DE.科目:czsx 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
科目:czsx 来源: 题型:
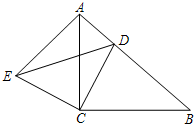 20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.
20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.科目:czsx 来源: 题型:
 (2013•吉林)如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
(2013•吉林)如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.| 2 |
| 2 |
科目:czsx 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.科目:czsx 来源: 题型:
 如图,△ABC中,∠ACB=90°,AC=BC=2,取斜边的中点,向斜边做垂线,画出一个新的等腰直角三角形,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边重叠为止,此时这个三角形的斜边长为
如图,△ABC中,∠ACB=90°,AC=BC=2,取斜边的中点,向斜边做垂线,画出一个新的等腰直角三角形,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边重叠为止,此时这个三角形的斜边长为| 1 |
| 4 |
| 1 |
| 4 |
科目:czsx 来源: 题型:
科目:czsx 来源:浙江省2013届八年级上学期期末考试数学卷 题型:选择题
如图,△ABC中,∠ACB = 90°,AC=BC=1,取斜边中点,向斜边做垂线,画出一个新的等腰直角三角形,此时这个三角形的斜边与BC垂直.如此继续下去,直到所画直角三角形的斜边再次与△ABC的BC边垂直为止,此时这个三角形的直角边长为 .
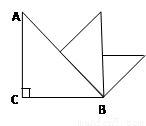
(第18题)
科目:czsx 来源:2015届北京市七年级下学期期末考试数学试卷(解析版) 题型:解答题
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
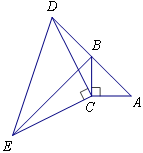
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE= cm;
(3)BE与AD有何位置关系?请说明理由.
科目:czsx 来源: 题型:

科目:czsx 来源:2011-2012学年河北保定市八年级第二学期期末数学试卷(解析版) 题型:填空题
如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边做垂线,画出一个新的等腰直角三角形,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边重叠为止,此时这个三角形的斜边长为__________.
