如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证答案解析
科目:czsx
来源:
题型:

如图,已知线段AB=12cm,点C是AB的中点,点D在直线AB上,且AB=4BD.求线段CD的长.
查看答案和解析>>
科目:czsx
来源:
题型:
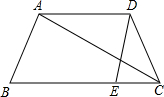
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
(1)填空:
+=
;
-=
.
(2)求作:
+.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,点A、B、P在以1为半径的⊙0上,点P为动点,AB=
,若△ABP是等腰三角形,则所有符合条件的点P有( )
查看答案和解析>>
科目:czsx
来源:
题型:
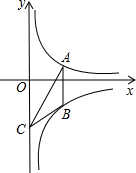
如图,点A在反比例函数
y=(x>0)的图象上,过A作AB⊥x轴与反比例函数
y=-(x>0)的图象交于点B,点C为y轴上任意一点,则△ABC的面积为
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知:AB=AC,直线m经过点A,点D、E是直线m上两个动点,连接BD、CE.

(1)如图1,若∠BAC=90°,BD⊥DE,CE⊥DE.求证:DE=BD+CE.
(2)如图2,若∠BAC=∠BDA=∠AEC,则(1)中的结论DE=BD+CE还成立吗?(只回答答案,不用证明)
(3)如图3,在(2)的条件下,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,是判定△DEF的形状,并证明你的判定.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,点D、E在△ABC的边BC上,AD=AE,BD=CE,求证:AB=AC.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,点C在线段AB上,△AMC和△CBN都是等边三角形,求证:
(1)
=;
(2)MD•EB=ME•DC.
查看答案和解析>>
科目:czsx
来源:
题型:

在△ABC中,AC=BC,∠ACB=90°,DG为△ABC的中位线.如图,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到DF,连接CF,过点F作FH⊥FC,交直线AB于点H.求证:FH=FC.
查看答案和解析>>
科目:czsx
来源:
题型:
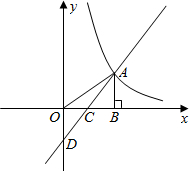
如图所示,在直角坐标系中,点A是反比例函数
y1=(x>0)的图象上一点,AB⊥x轴的正半轴于B点,C是OB的中点;一次函数y
2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S
△AOD=4.
(1)求反比例函数和一次函数的解析式;
(2)观察图象,请指出,当y
1≥y
2时,x的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
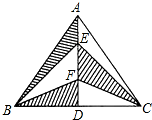
如图,已知在△ABC中,AB=AC=10cm,BC=12cm,点E、F都在中线AD上,连接EB、EC、FB、FC,则图中阴影部分的面积为
24cm2
24cm2
.
查看答案和解析>>
科目:czsx
来源:
题型:
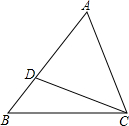
如图,点D在△ABC的边AB上,连接CD,且∠ACD=∠B.
(1)△ABC与△ACD相似吗?为什么?
(2)若AD=4,AC=6,求AB的长.
查看答案和解析>>
科目:czsx
来源:
题型:
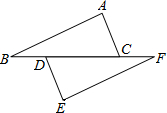
如图,点B、D、C、F在同一直线上,AB∥EF,AB=EF,要使∠A=∠E,应该添加的条件是
BC=FD(答案不唯一)
BC=FD(答案不唯一)
.
查看答案和解析>>
科目:czsx
来源:
题型:
探究问题
(1)方法感悟:
一班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
方案(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;感悟解题方法,并完成下列填空:
解:在如图所示的两个三角形△DEC和△ABC中:DC=AC,∠
ACB
ACB
=∠
DCE
DCE
(对顶角相等),EC=BC,∴△DEC≌△ABC
(SAS)
(SAS)
,∴DE=AB(全等三角形对应边相等),即DE的距离即为AB的长.
(2)方法迁移:
方案(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.请你说明理由.
(3)问题拓展:
方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是
作∠ABC=∠EDC=90°
作∠ABC=∠EDC=90°
;若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立?
成立
成立
.
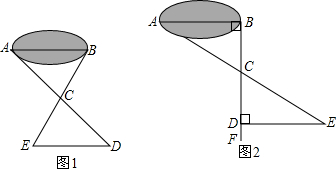
查看答案和解析>>
科目:czsx
来源:
题型:
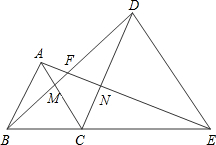
如图,点B,C,E,在同一直线上,点A,D在直线CE同侧,AB=AC,EC=ED,∠BAC=∠CED=60°,AE与BD交于点F,AC与BD交于点M,DC与AE交于N,则:
(1)△BCD≌△
ACE
ACE
;
(2)∠AFB=
60
60
(度);
(3)△CMD≌△
CNE
CNE
.
查看答案和解析>>
科目:czsx
来源:
题型:
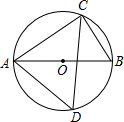
如图,点A、B、C、D在⊙O上,AB为⊙O的直径,∠BAC=35°,求∠ADC的度数.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(下面两小题的结果都精确到0.1米,参考数据:
≈1.732)
(1)若修建的斜坡BE的坡度为1:0.8,则平台DE的长为
14.0
14.0
米;
(2)斜坡前的池塘内有一座建筑物GH,小明在平台E处测得建筑物顶部H的仰角(即∠HEM)为30°,测得建筑物顶部H在池塘中倒影H′的俯角为45°(即∠H′EM),测得点B、C、A、G、H、H′在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,求建筑物GH的高和AG的长.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角三角形DCE中∠DCE是直角,点D在线段AC上,M是线段BE的中点,N是线段AD的中点.
(1)连接BD,AE,求证:△BCD≌△ACE;
(2)猜想图1中的MN与OM的数量关系(直接写出结果);
(3)将△DCE绕点C逆时针旋转α(0°<α<90°)(备用图2)后,其他条件不变,(2)中的结论仍然成立吗?若是,画出图形并证明;若不是,说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,以坐标原点O为圆心半径为2画⊙O.
(1)若A的坐标为(4,0)时,过点A的直线切⊙O于点P,交y轴于点B.求线段AP的长.
(2)求出AB所在的直线解析式.
(3)如图,若P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴交与点A,与y轴交于点B.请问:在⊙O是否存在一点Q,使得以Q,O,A,P为顶点的四边形是一个平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
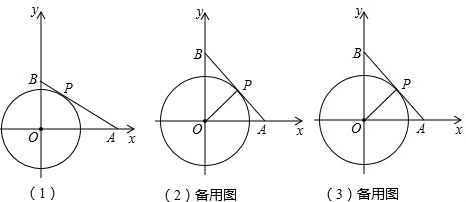
查看答案和解析>>
科目:czsx
来源:
题型:

如图,点A,B的坐标分别为(2,-5)和(5,-5),抛物线y=a(x-m)
2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D横坐标的最大值为
10
10
.
查看答案和解析>>
科目:czsx
来源:
题型:
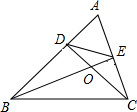
如图,已知在△ABC中,点D、E分别在AB、AC上,且AD•AB=AE•AC,CD与BE相交于点O.
(1)求证:△AEB∽△ADC;
(2)求证:
=.
查看答案和解析>>

 如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC. 如图,点A在反比例函数y=
如图,点A在反比例函数y=
 在△ABC中,AC=BC,∠ACB=90°,DG为△ABC的中位线.如图,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到DF,连接CF,过点F作FH⊥FC,交直线AB于点H.求证:FH=FC.
在△ABC中,AC=BC,∠ACB=90°,DG为△ABC的中位线.如图,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到DF,连接CF,过点F作FH⊥FC,交直线AB于点H.求证:FH=FC. 如图所示,在直角坐标系中,点A是反比例函数y1=
如图所示,在直角坐标系中,点A是反比例函数y1= 如图,已知在△ABC中,AB=AC=10cm,BC=12cm,点E、F都在中线AD上,连接EB、EC、FB、FC,则图中阴影部分的面积为
如图,已知在△ABC中,AB=AC=10cm,BC=12cm,点E、F都在中线AD上,连接EB、EC、FB、FC,则图中阴影部分的面积为
 如图,点B,C,E,在同一直线上,点A,D在直线CE同侧,AB=AC,EC=ED,∠BAC=∠CED=60°,AE与BD交于点F,AC与BD交于点M,DC与AE交于N,则:
如图,点B,C,E,在同一直线上,点A,D在直线CE同侧,AB=AC,EC=ED,∠BAC=∠CED=60°,AE与BD交于点F,AC与BD交于点M,DC与AE交于N,则: 如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(下面两小题的结果都精确到0.1米,参考数据:
如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(下面两小题的结果都精确到0.1米,参考数据:

 如图,点A,B的坐标分别为(2,-5)和(5,-5),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D横坐标的最大值为
如图,点A,B的坐标分别为(2,-5)和(5,-5),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D横坐标的最大值为 如图,已知在△ABC中,点D、E分别在AB、AC上,且AD•AB=AE•AC,CD与BE相交于点O.
如图,已知在△ABC中,点D、E分别在AB、AC上,且AD•AB=AE•AC,CD与BE相交于点O.