科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| k |
| x |
| 2 |
 取值范围.
取值范围.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:


科目:czsx 来源: 题型:
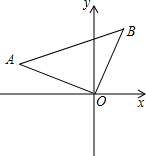 ,1).
,1).科目:czsx 来源: 题型:
| 869 |
科目:czsx 来源:2008年安徽省合肥市庐阳区中考数学试卷(解析版) 题型:解答题

科目:czsx 来源:2012年辽宁省建平县八年级单科数学竞赛卷(带解析) 题型:解答题
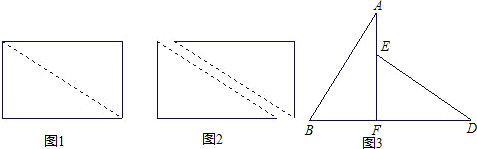
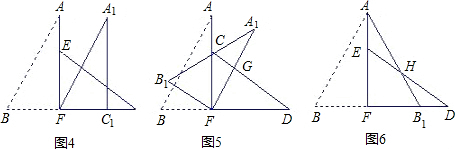
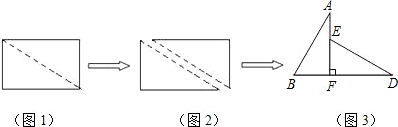
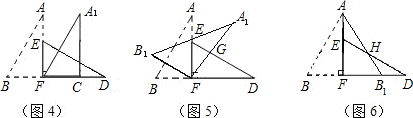
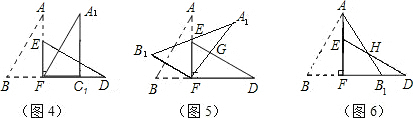
如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合.(在图3至图6中统一用F表示)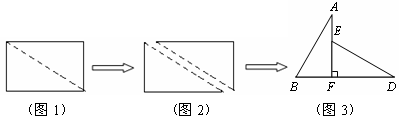
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请说明:AH=DH.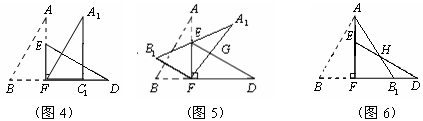
科目:czsx 来源:第23章《二次函数与反比例函数》中考题集(35):23.5 二次函数的应用(解析版) 题型:解答题

科目:czsx 来源:第20章《二次函数和反比例函数》中考题集(35):20.5 二次函数的一些应用(解析版) 题型:解答题

科目:czsx 来源:第2章《二次函数》中考题集(36):2.4 二次函数的应用(解析版) 题型:解答题

科目:czsx 来源:2012-2013学年江西省景德镇市九年级下学期第二次质检数学试卷(解析版) 题型:解答题
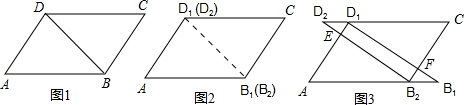
有4张形状、大小和质地都相同的卡片,正面分别写有字母A、B、C、D和一个算式,背面完全一致.如图所示,将这4张卡片背面向上洗匀,从中随机抽取1张,不放回,接着再随机抽取1张.

(1)请用画树形图或列表法表示出所有的可能结果;(卡片可用A、B、C、D表示)
(2)将“第一张卡片上的算式是正确,同时第二张卡片上的算式是错误”记为事件A,求事件A的概率.
科目:czsx 来源: 题型:
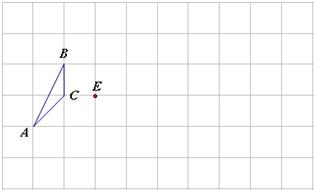
已知:如图,在△ABC中,AB=AC,∠BAC=30°.点D为△ABC内一点,
且DB=DC,∠DCB=30°.点E为BD延长线上一点,且AE=AB

1.求∠ADE的度数
2.若点M在DE上,且DM=DA,
求证:ME=DC.
科目:czsx 来源:第34章《二次函数》中考题集(39):34.4 二次函数的应用(解析版) 题型:解答题