精英家教网 >
试题搜索列表 >设函数y=f(x)的定义域为r,对任意的x,y有f(x-y)=f(x),且f(2)=1,当>0时,f(x)>0(1)求f(0)的值
设函数y=f(x)的定义域为r,对任意的x,y有f(x-y)=f(x),且f(2)=1,当>0时,f(x)>0(1)求f(0)的值答案解析
科目:gzsx
来源:
题型:044
设函数f(x)的定义域为R,对任意数a、b有f(a)+f(b)= ,且
,且
(1)求证:f(-x)=f(x)=-f(p-x)
(2)若0£x£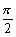 时,f(x)>0,求证:f(x)在[0,p]上单调递减;
时,f(x)>0,求证:f(x)在[0,p]上单调递减;
(3)求f(x)的最小周期并加以证明.
查看答案和解析>>
科目:gzsx
来源:数学教研室
题型:044
设函数f(x)的定义域为R
,对任意数a、b有f(a)+f(b)=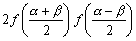
,
且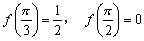
(1)求证:f(-x)=f(x)=-f(p-x)
(2)若0£x£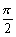 时,f(x)>0,求证:f(x)在[0,p]上单调递减;
时,f(x)>0,求证:f(x)在[0,p]上单调递减;
(3)求f(x)的最小周期并加以证明.
查看答案和解析>>
科目:gzsx
来源:数学教研室
题型:044
已知函数f(x)的定义域为R,对任意实数m,n均有f(m+n)=f(m)+f(n)-1,且f(-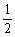 )=2,又当x>-
)=2,又当x>- 时,有f(x)>0.
时,有f(x)>0.
(1)求f(- )的值;
)的值;
(2)证明:f(x)是单调递增函数;
(3)解不等式:1+f( )
) f(1)+f(x).
f(1)+f(x).
查看答案和解析>>
科目:gzsx
来源:
题型:044
已知函数f(x)的定义域为R,对任意实数m,n均有f(m+n)=f(m)+f(n)-1,且f(-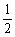 )=2,又当x>-
)=2,又当x>- 时,有f(x)>0.
时,有f(x)>0.
(1)求f(- )的值;
)的值;
(2)证明:f(x)是单调递增函数;
(3)解不等式:1+f( )
) f(1)+f(x).
f(1)+f(x).
查看答案和解析>>
科目:gzsx
来源:
题型:
(2008•南汇区二模)设函数y=f(x)的定义域为R,对任意实数x,y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4.
(1)求证:y=f(x)为奇函数;
(2)在区间[-9,9]上,求y=f(x)的最值.
查看答案和解析>>
科目:gzsx
来源:
题型:
设函数f(x)的定义域为R,对任意的实数x,y都有f(x+y)=f(x)+f(y);当x<0时,f(x)<0,且f(1)=1.
(1)判断并证明f(x)在(-∞,+∞)上的单调性;
(2)若数列{an}满足:0<a1<1,且2-an+1=f(2-an),证明:对任意的n∈N*,0<an<1.
查看答案和解析>>
科目:gzsx
来源:
题型:
设函数f(x)的定义域为R,对任意实数x、y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4.
(1)求证: f(x)为奇函数;
(2)在区间[-9,9]上,求f(x)的最值.
查看答案和解析>>
科目:gzsx
来源:广东省汕头市东厦中学2007-2008年度高三级第二次质量检测、数学文科
题型:044
设函数f(x)的定义域为R,对任意实数x、y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0,且f(3)=-4.
(1)求f(0),f(1)的值
(2)求证:f(x)为奇函数;
(3)在区间[-9,9]上,求f(x)的最值.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
设函数y=f(x)的定义域为R,对任意实数x,y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4.
(1)求证:y=f(x)为奇函数;
(2)在区间[-9,9]上,求y=f(x)的最值.
查看答案和解析>>
科目:gzsx
来源:高中数学全解题库(国标苏教版·必修4、必修5) 苏教版
题型:044
设函数y=f(x)的定义域为R,对任意实数m,n,有f(m+n)=f(m)f(n),且当x<0时,f(x)>1数列{an}满足a1=f(0),且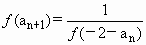 (n∈N*).
(n∈N*).
(1)求证:y=f(x)在R上单调递减.
(2)求数列{an}的通项公式.
(3)是否存在正数k,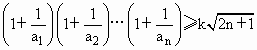 对一切n∈N*均成立?若存在.试求出k的最大值并证明:若不存在,请说明理由.
对一切n∈N*均成立?若存在.试求出k的最大值并证明:若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年广东省揭阳一中高三(上)第二次段考数学试卷(解析版)
题型:解答题
设函数f(x)的定义域为R,对任意的实数x,y都有f(x+y)=f(x)+f(y);当x<0时,f(x)<0,且f(1)=1.
(1)判断并证明f(x)在(-∞,+∞)上的单调性;
(2)若数列{an}满足:0<a1<1,且2-an+1=f(2-an),证明:对任意的n∈N*,0<an<1.
查看答案和解析>>
科目:gzsx
来源:101网校同步练习 高三数学 苏教版(新课标·2004年初审) 苏教版
题型:044
设函数f(x)的定义域为R,对任意实数x、y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4.
(1)求证:f(x)为奇函数;
(2)在区间[-9,9]上,求f(x)的最值.
查看答案和解析>>
科目:gzsx
来源:
题型:044
(
广东六校联考模拟)设函数f(x)的定义域为R,对任意实数x、y都有f(x+y)=f(x)+f(y),当x>0时,f(x)>0且f(2)=6.
(1)
求证:函数f(x)为奇函数;
(2)
证明函数f(x)在R上是增函数;
(3)
在区间[-4,4]上,求f(x)的最值.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
设函数f(x)的定义域为R,对任意的实数x,y都有f(x+y)=f(x)+f(y);当x<0时,f(x)<0,且f(1)=1.
(1)判断并证明f(x)在(-∞,+∞)上的单调性;
(2)若数列{an}满足:0<a1<1,且2-an+1=f(2-an),证明:对任意的n∈N*,0<an<1.
查看答案和解析>>
科目:gzsx
来源:南汇区二模
题型:解答题
设函数y=f(x)的定义域为R,对任意实数x,y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4.
(1)求证:y=f(x)为奇函数;
(2)在区间[-9,9]上,求y=f(x)的最值.
查看答案和解析>>
科目:gzsx
来源:2008年上海市南汇区高考数学二模试卷(文理合卷)(解析版)
题型:解答题
设函数y=f(x)的定义域为R,对任意实数x,y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4.
(1)求证:y=f(x)为奇函数;
(2)在区间[-9,9]上,求y=f(x)的最值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)的定义域为R,对任意实数x,y都有f(x+y)=f(x)+f(y)+
,且
f()=0,当x>
时,f(x)>0.
(1)求f(1)+f(2)+…+f(n)(n∈N
*);
(2)判断函数f(x)的单调性并证明.
查看答案和解析>>
科目:gzsx
来源:
题型:
21、已知函数y=f(x)的定义域为R,对任意x、x′∈R均有f(x+x′)=f(x)+f(x′),且对任意x>0,都有f(x)<0,f(3)=-3.
(1)试证明:函数y=f(x)是R上的单调减函数;
(2)试证明:函数y=f(x)是奇函数;
(3)试求函数y=f(x)在[m,n](m、n∈Z,且mn<0)上的值域.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)的定义域为R,对任意的实数x,y都有f(x+y)=f(x)+f(y)+
,且f(
)=0,当x>
时,f(x)>0.
(1)求f(1);
(2)判断函数f(x)的单调性,并证明.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数y=f(x)的定义域为R,对任意x,x′∈R,均有f(x+x′)=f(x)+f(x′),且对任意x>0都有f(x)<0,f(3)=-3.
(1)试证明:函数y=f(x)在R上是单调函数;
(2)判断y=f(x)的奇偶性,并证明.
(3)解不等式f(x+3)+f(4x)≤2.
(4)试求函数y=f(x)在[m,n](mn<0且m,n∈R)上的值域.
查看答案和解析>>

![]() ,且
,且![]()
![]() 时,f(x)>0,求证:f(x)在[0,p]上单调递减;
时,f(x)>0,求证:f(x)在[0,p]上单调递减;![]() 时,f(x)>0,求证:f(x)在[0,p]上单调递减;
时,f(x)>0,求证:f(x)在[0,p]上单调递减;![]() )的值;
)的值;![]() )
)![]() f(1)+f(x).
f(1)+f(x).![]() )=2,又当x>-
)=2,又当x>-![]() 时,有f(x)>0.
时,有f(x)>0.![]() )的值;
)的值;![]() )
)![]() f(1)+f(x).
f(1)+f(x).![]() (n∈N*).
(n∈N*).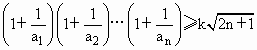 对一切n∈N*均成立?若存在.试求出k的最大值并证明:若不存在,请说明理由.
对一切n∈N*均成立?若存在.试求出k的最大值并证明:若不存在,请说明理由.