
科目:czsx 来源: 题型:
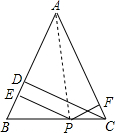 【老题重现】
【老题重现】| AB×PE |
| 2 |
| AC×PF |
| 2 |
| AB×CD |
| 2 |
科目:czsx 来源:2010年山东省青岛市李沧区中考数学二模试卷(解析版) 题型:解答题

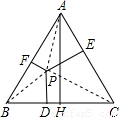
科目:czsx 来源:2013年山东省青岛市中考数学模拟试卷(三)(解析版) 题型:解答题



科目:czsx 来源: 题型:解答题
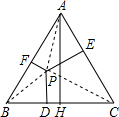
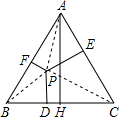
 求证:等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.
求证:等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.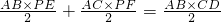
科目:czsx 来源:2011-2012学年北京101中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
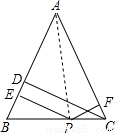
如图所示,直角梯形 的直角顶点
的直角顶点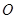 是坐标原点,边
是坐标原点,边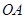 、
、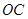 分别在
分别在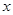 轴、
轴、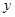 轴的正半轴上,
轴的正半轴上,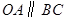 ,
,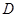 是
是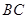 上一点,
上一点,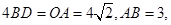
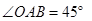 ,其中点
,其中点 、
、 分别是线段
分别是线段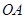 、
、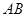 上的两个动点,且始终保持
上的两个动点,且始终保持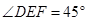 。
。
【小题1】直接写出点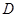 的坐标
的坐标
【小题2】求证: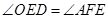 ;
;
【小题3】当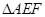 是等腰三角形时,△AEF关于直线EF的对称图形为
是等腰三角形时,△AEF关于直线EF的对称图形为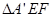 ,求
,求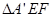 与五边形OEFBC的重叠部分的面积.
与五边形OEFBC的重叠部分的面积.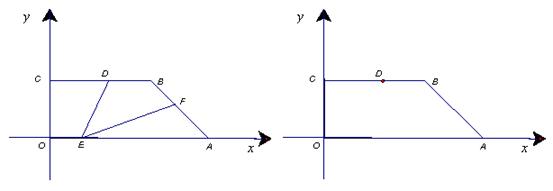
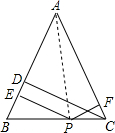
备用图
科目:czsx 来源: 题型:

科目:czsx 来源:2012届辽宁省盘锦市第一完全中学九年级第一次中考模拟数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系xOy中,一次函数 的图象与反比例函数图象的一个交点为A
的图象与反比例函数图象的一个交点为A .
.
【小题1】求反比例函数的解析式;
【小题2】若点P是坐标轴上任意一点,且满足PA=OA,求出点P的坐标.
科目:czsx 来源: 题型:
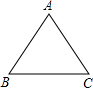
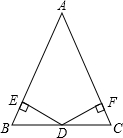 求证:等腰三角形底边上的中点到两腰的距离相等.结合所给图形,把“已知”、“求证”补充完整,并完成证明过程.
求证:等腰三角形底边上的中点到两腰的距离相等.结合所给图形,把“已知”、“求证”补充完整,并完成证明过程.科目:czsx 来源: 题型:阅读理解
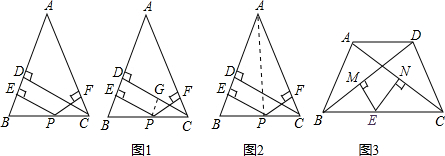
科目:czsx 来源: 题型:解答题

科目:czsx 来源:2010年广东省深圳市宝安区中考数学一模试卷(解析版) 题型:解答题
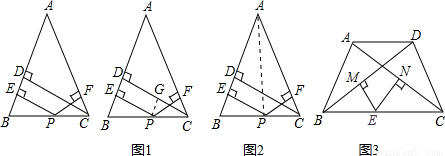
科目:czsx 来源: 题型:阅读理解