科目:gzsx
来源:
题型:
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
查看答案和解析>>
科目:gzsx
来源:
题型:
数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=3x+1上,n∈N*.
(Ⅰ)当实数t为何值时,数列{an}是等比数列?
(Ⅱ)在(Ⅰ)的结论下,设bn=log4an+1,cn=an+bn,Tn是数列{cn}的前n项和,求Tn.
查看答案和解析>>
科目:gzsx
来源:
题型:
数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N
*.
(1)当实数t为何值时,数列{a
n}是等比数列?
(2)在(1)的结论下,设b
n=log
3a
n+1,T
n是数列{
}的前n项和,求T
2013的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•肇庆二模)数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N
*.
(1)若数列{a
n}是等比数列,求实数t的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项均不为0的数列{c
n}中,所有满足c
i•c
i+1<0的整数i的个数称为这个数列{c
n}的“积异号数”,令
cn=(n∈N
*),在(2)的条件下,求数列{c
n}的“积异号数”.
查看答案和解析>>
科目:gzsx
来源:
题型:
数列{an}的前n项和记为Sn,a1=t,an+1=Sn+1(n∈N*),数列{bn}为等差数列,且b5=9,b7=13.
(I)t为何值,数列{an}是等比数列?
(II)在(I)的条件下,若cn=an•bn(n∈N*),设TN为数列{cn}的前n项和,求Tn.
查看答案和解析>>
科目:gzsx
来源:
题型:
数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N.
(I)当实数t为何值时,数列{a
n}是等比数列?
(Ⅱ)在(I)的结论下,设b
n=log
3a
n+1,T
n是数列
的前n项和,求T
2012的值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年广东省佛山市高明一中高三(上)第一次月考数学试卷(理科)(解析版)
题型:解答题
数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N
*.
(1)若数列{a
n}是等比数列,求实数t的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项均不为0的数列{c
n}中,所有满足c
i•c
i+1<0的整数i的个数称为这个数列{c
n}的“积异号数”,令

(n∈N
*),在(2)的条件下,求数列{c
n}的“积异号数”.
查看答案和解析>>
科目:gzsx
来源:2007年山东省烟台市莱州一中高考数学三模试卷(理科)(解析版)
题型:解答题
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
查看答案和解析>>
科目:gzsx
来源:2011-2012学年山东省聊城市阳谷县华阳中学高三(下)3月月考数学试卷(文科)(解析版)
题型:解答题
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
查看答案和解析>>
科目:gzsx
来源:2006年四川省高考数学试卷(文科)(解析版)
题型:解答题
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年河南省中原名校高二(上)期中数学试卷(理科)(商丘一高命题)(解析版)
题型:解答题
数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N.
(I)当实数t为何值时,数列{a
n}是等比数列?
(Ⅱ)在(I)的结论下,设b
n=log
3a
n+1,T
n是数列

的前n项和,求T
2012的值.
查看答案和解析>>
科目:gzsx
来源:2010年北京市重点中学高考模拟数学试卷(理科)(解析版)
题型:解答题
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
数列{an}的前n项和记为Sn,a1=t,an+1=Sn+1(n∈N*),数列{bn}为等差数列,且b5=9,b7=13.
(I)t为何值,数列{an}是等比数列?
(II)在(I)的条件下,若cn=an•bn(n∈N*),设TN为数列{cn}的前n项和,求Tn.
查看答案和解析>>
科目:gzsx
来源:上海市模拟题
题型:解答题
数列{a
n}的前n项和记为S
n,a
1=t,点
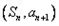
在直线y=2x+1上,
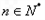
。
(1)若数列{a
n}是等比数列,求实数t的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项均不为0的数列{c
n}中,所有满足
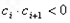
的整数

的个数称为这个数列
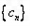
的”,令
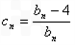
(
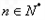
),在(2)的条件下,求数列
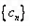
的“积异号数”。
查看答案和解析>>
科目:gzsx
来源:2011年高三数学第一轮基础知识训练(31)(解析版)
题型:解答题
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年福建省莆田四中高二(上)辅优周练数学试卷(二)(解析版)
题型:解答题
数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N
*.
(1)若数列{a
n}是等比数列,求实数t的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项均不为0的数列{c
n}中,所有满足c
i•c
i+1<0的整数i的个数称为这个数列{c
n}的“积异号数”,令

(n∈N
*),在(2)的条件下,求数列{c
n}的“积异号数”.
查看答案和解析>>
科目:gzsx
来源:广东省高考数学一轮复习:6.8 数列的综合问题(解析版)
题型:解答题
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年广东省佛山市高明一中高三(上)第一次月考数学试卷(理科)(解析版)
题型:解答题
数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N
*.
(1)若数列{a
n}是等比数列,求实数t的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项均不为0的数列{c
n}中,所有满足c
i•c
i+1<0的整数i的个数称为这个数列{c
n}的“积异号数”,令

(n∈N
*),在(2)的条件下,求数列{c
n}的“积异号数”.
查看答案和解析>>
科目:gzsx
来源:2012年陕西省西安市西工大附中高考数学一模试卷(理科)(解析版)
题型:解答题
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年湖北省武汉市部分重点中学高三(上)起点考试数学试卷(文科)(解析版)
题型:解答题
数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N.
(I)当实数t为何值时,数列{a
n}是等比数列?
(Ⅱ)在(I)的结论下,设b
n=log
3a
n+1,T
n是数列

的前n项和,求T
2012的值.
查看答案和解析>>

 (n∈N*),在(2)的条件下,求数列{cn}的“积异号数”.
(n∈N*),在(2)的条件下,求数列{cn}的“积异号数”. 的前n项和,求T2012的值.
的前n项和,求T2012的值.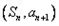 在直线y=2x+1上,
在直线y=2x+1上,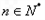 。
。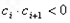 的整数
的整数 的个数称为这个数列
的个数称为这个数列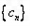 的”,令
的”,令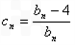 (
(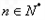 ),在(2)的条件下,求数列
),在(2)的条件下,求数列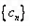 的“积异号数”。
的“积异号数”。 (n∈N*),在(2)的条件下,求数列{cn}的“积异号数”.
(n∈N*),在(2)的条件下,求数列{cn}的“积异号数”. (n∈N*),在(2)的条件下,求数列{cn}的“积异号数”.
(n∈N*),在(2)的条件下,求数列{cn}的“积异号数”. 的前n项和,求T2012的值.
的前n项和,求T2012的值.