
科目:czsx 来源:2007年安徽省安庆市一中理科实验班招生考试数学试卷(解析版) 题型:选择题
科目:czsx 来源: 题型:单选题
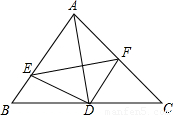
 如图,AD是△ABC的中线,E、F分别在AB、AC上(且E,F不与端点重合),且DE⊥DF,则
如图,AD是△ABC的中线,E、F分别在AB、AC上(且E,F不与端点重合),且DE⊥DF,则科目:czsx 来源: 题型:
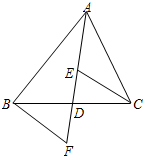 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:
如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:科目:czsx 来源: 题型:
 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:①△BDF≌△CDE;②CE=BF;③BF∥CE;④△ABD和△ACD面积相等.其中正确的有( )
如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:①△BDF≌△CDE;②CE=BF;③BF∥CE;④△ABD和△ACD面积相等.其中正确的有( )科目:czsx 来源: 题型:
 如图,AD是△ABC的中线,BE是△ABD的中线.
如图,AD是△ABC的中线,BE是△ABD的中线.科目:czsx 来源: 题型:
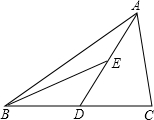 如图,AD是△ABC的中线,BE是△ABD的中线
如图,AD是△ABC的中线,BE是△ABD的中线