练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >若圆(x+a)2+(y-1)2＝a2在x

    若圆(x+a)2+(y-1)2＝a2在x答案解析

    科目：gzsx 来源： 题型：单选题

    若圆(x+a)2+(y-1)2＝a2在x轴上方，则


    1. A.
      |a|＜1
    2. B.
      |a|≤1
    3. C.
      0＜|a|＜1
    4. D.
      0≤|a|＜1

    查看答案和解析>>

    科目：gzsx 来源：浙江省期中题 题型：单选题

    △ABC的三内角A,B,C所对边的长分别为a,b,c，若直线bx+(a-c)y+1=0与直线(a-b)x-(a+c)y+1=0垂直，则角C的大小为                     
    [     ]
    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2006•黄浦区二模）设a为正数，直角坐标平面内的点集A={（x，y）|x，y，a-x-y是三角形的三边长}．
    （1）画出A所表示的平面区域；
    （2）在平面直角坐标系中，规定a∈Z，且y∈Z时，（x，y）称为格点，当a=8时，A内有几个格点（本小题只要直接写出结果即可）；
    （3）点集A连同它的边界构成的区域记为
    .
    A
    ，若圆{(x，y)|(x-p)2+(x-q)2=r2}⊆
    .
    A
    (r＞0)    ，求r的最大值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若圆C的半径为1，圆心在第一象限，且与直线3x-4y=0和y轴相切，则该圆的标准方程是（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若圆C的半径为1，圆心在第一象限，且与直线4x-3y=0和x轴都相切，则该圆的标准方程是（　　）
    A、（x-2）2+（y-1）2=1B、（x-2）2+（y+1）2=1C、（x+2）2+（y-1）2=1D、（x-3）2+（y-1）2=1

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点Bn（n，yn），…（n∈N+）是某直线l上的点，以Bn为圆心作圆．所作的圆与x轴交于An和An+1两点，记An、An+1的横坐标分别为xn、xn+1．其中x1=a（0＜a≤1）
    （1）证明：xn+2-xn是常数，并求数列{xn}的通项公式；
    （2）若l的方程为y=
    1
    4
    x+
    1
    12
    ，试问在△AnBnAn+1(n∈N+)    中是否存在直角三角形，若存在，求出a的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知圆O：x2+y2=1，点P在直线l：2x+y-3=0上，过点P作圆O的两条切线，A，B为两切点．
    （1）求切线长PA的最小值，并求此时点P的坐标；
    （2）点M为直线y=x与直线l的交点，若在平面内存在定点N（不同于点M），满足：对于圆 O上任意一点Q，都有
    QN
    QM
    为一常数，求所有满足条件的点N的坐标．
    （3）求
    PA
    •
    PB
    的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    P为椭圆C：
    y2
    a2
    +
    x2
    b2
    =1(a＞b＞0)    上一点，A、B为圆O：x2+y2=b2上的两个不同的点，直线AB分别交x轴，y轴于M、N两点且
    PA
    •
    OA
    =0    ，
    PB
    •
    OB
    =0    ，O为坐标原点．
    （1）若椭圆的准线为y=±
    25
    3
    ，并且
    a2
    |
    OM
    |2
    +
    b2
    |
    ON
    |2
    =
    25
    16
    ，求椭圆C的方程．
    （2）椭圆C上是否存在满足
    PA
    •
    PB
    =0    的点P？若存在，求出存在时a，b满足的条件；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （选做题）在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．
    A．选修4-1：几何证明选讲
    如图，⊙O的半径OB垂直于直径AC，M为AO上一点，BM的延长线交⊙O于N，过
    N点的切线交CA的延长线于P．
    （1）求证：PM2=PA•PC；
    （2）若⊙O的半径为2
    		3
    ，OA=
    		3
    OM，求MN的长．
    B．选修4-2：矩阵与变换
    曲线x2+4xy+2y2=1在二阶矩阵M=
    .
    1a
    b1
    .
    的作用下变换为曲线x2-2y2=1，求实数a，b的值；
    C．选修4-4：坐标系与参数方程
    在极坐标系中，圆C的极坐标方程为ρ=
    		2
    cos(θ+
    π
    4
    )    ，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
    x=1+
    4
    5
    t 
    y=-1-
    3
    5
    t 
    （t为参数），求直线l被圆C所截得的弦长．
    D．选修4-5：不等式选讲
    设a，b，c均为正实数．
    （1）若a+b+c=1，求a2+b2+c2的最小值；
    （2）求证：
    1
    2a
    +
    1
    2b
    +
    1
    2c
    ≥
    1
    b+c
    +
    1
    c+a
    +
    1
    a+b
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若圆C1：x2+y2=1和圆C2：(x+4)2+(y-a)2=25外切，则a的值为
    ±2
    		5
    ±2
    		5
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆
    x2
    2b2
    +
    y2
    b2
    =1(b＞0)
    （1）若圆(x-2)2+(y-1)2=
    20
    3

    （2）与椭圆相交于A、B两点且线段AB恰为圆的直径，求椭圆方程；
    （3）设L为过椭圆右焦点F的直线，交椭圆于M、N两点，且L的倾斜角为60°．求
    |MF|
    |NF|
    的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若圆C的半径为1，圆心在第一象限，且与直线4x-3y=0和x轴相切，则该圆的标准方程是（　　）
    A、(x-3)2+(y-
    7
    3
    )2=1
    B、（x-2）2+（y-1）2=1
    C、（x-1）2+（y-3）2=1
    D、(x-
    3
    2
    )2+(y-1)2=1

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称，过点C（-a，a）的圆P与y轴相切，则圆心P的轨迹方程为（　　）
    A、y2-4x+4y+8=0B、y2-2x-2y+2=0C、y2+4x-4y+8=0D、y2-2x-y-1=0

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知圆C1：x2+y2-2x-4y+4=0
    （Ⅰ）若直线l：x+2y-4=0与圆C1相交于A，B两点．求弦AB的长；
    （Ⅱ）若圆C2经过E（1，-3），F（0，4），且圆C2与圆C1的公共弦平行于直线2x+y+1=0，求圆C2的方程．
    （Ⅲ）求证：不论实数λ取何实数时，直线l1：2λx-2y+3-λ=0与圆C1恒交于两点，并求出交点弦长最短时直线l1的方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知圆C：（x+3）2+（y-4）2=4．
    （1）若直线l1过点A（-1，0），且与圆C相切，求直线l1的方程；
    （2）若圆D的半径为4，圆心D在直线l2：2x+y-2=0上，且与圆C内切，求圆D的方程．

    查看答案和解析>>

    科目：gzsx 来源：2011-2012学年安徽省淮北市高三第一次模拟考试文科数学 题型：选择题

    若圆C的半径为1，圆心在第一象限，且与直线4x-3y=0和x轴都相切，则该圆的标准方程是    (    )

      A. (x-2)2+(y-1)2=1     B、 (x-2)2+(y-3)2=1

      C. (x-3)2+(y-2)2=1     D．（x-3)2+(y-1)2=1

     

    查看答案和解析>>

    科目：gzsx 来源：2011-2012学年山东省济宁市高三11月月考理科数学试卷 题型：选择题

    若圆C的半径为1，圆心在第一象限，且与直线4x-3y=0和x轴都相切，则该圆的标准方程是　（    ）

    A．（x-2）2+（y-1）2=1                        B．（x-2） 2+（y+1） 2=1

    C．（x+2） 2+（y-1） 2=1                       D．（x-3） 2+（y-1） 2=1

     

    查看答案和解析>>

    科目：gzsx 来源：2013届安徽省安庆市三校联考高一上学期期末考试数学 题型：选择题

    若圆(x-3)2+(y+5)2=r2上有且只有两个点到直线4x-3y=2的距离等于1，则半径r的范围是(    )   

    A．（4，6）   B．[4，6]                C．[4，6]     D．（4，6]

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若圆(x-3)2+(y+5)2=r2上有且只有两个点到直线4x-3y=2的距离等于1，则半径r的取值范围是(    )

    A.(4，6)               B.［4,6)               C.(4,6］              D.［4,6］

    查看答案和解析>>

    科目：gzsx 来源：2012届江西省上饶市高三第二次模拟考试理科数学试卷（解析版） 题型：解答题

    （14分）已知：圆C：x2＋（y－a）2＝a2（a＞0），动点A在x轴上方，圆A与x轴相切，且与圆C外切于点M

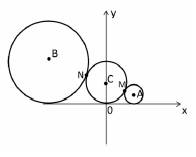
        （1）若动点A的轨迹为曲线E，求曲线E的方程；

        （2）动点B也在x轴上方，且A，B分别在y轴两侧．圆B与x轴相切，且与圆C外切于点N．若圆A，圆C，圆B的半径成等比数列，求证：A，C，B三点共线；

        （3）在（2）的条件下，过A，B两点分别作曲线E的切线，两切线相交于点T，若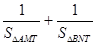的最小值为2，求直线AB的方程．

     

    查看答案和解析>>