如图14所示,BA ⊥AC, DC ⊥AC, 要使△ABC ≌△CDA, 现已有 和 条件,还需添加什么条件(最直接的)才能保证结论成立? 　　 (1)AB=CD(SAS);(2)答案解析

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

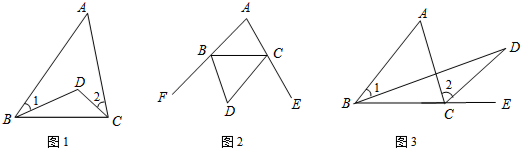
如图14所示，在直角坐标系中，O是坐标原点，点A在y轴正半轴上，二次函数y=ax²+[x/6]+c的图象F交x轴于B、C两点，交y轴于M点，其中B（-3，0），M（0，-1）。已知AM=BC。

[1]求二次函数的解析式；

[2]证明：在抛物线F上存在点D，使A、B、C、D四点连接而成的四边形恰好是平行四边形，并请求出直线BD的解析式；

[3]在[2]的条件下，设直线l过D且分别交直线BA、BC于不同的P、Q两点，AC、BD相交于N。

①若直线l⊥BD，如图14所示，试求[1/BP]+[1/BQ]的值；

②若l为满足条件的任意直线。如图15所示，①中的结论还成立吗？若成立，证明你的猜想；若不成立，请举出反例。

 

科目：czsx 来源：2011—2012学年广东湛江八年级上学期第三次月考数学试卷（带解析） 题型：解答题

科目：czsx 来源：2013届广东湛江八年级上学期第三次月考数学试卷（解析版） 题型：解答题

科目：czsx 来源：2012届河北石家庄初中毕业班教学质量检测数学试卷（带解析） 题型：解答题

科目：czsx 来源： 题型：

如图14所示，在△ABC中，AD⊥BC，请你添加一个条件，写出一个正确结论(不在图中添加辅助线)．条件是________­­­­­­­­_­­­______，结论为__________．

科目：czsx 来源： 题型：

某校为外国留学生举办“唱汉语歌曲”比赛，设优秀奖、鼓励奖共12名，其中优秀奖不少于6名.学校购买“脸谱”和“中国结”作为奖品，优秀奖和鼓励奖分别奖励“脸谱”和“中国结”各一个，费用信息如图14所示．
【小题1】请求出一个“脸谱”和一个“中国结”各多少元？
【小题2】若购买奖品费用不超过500元，则本次活动优秀奖和鼓励奖名额应如何设置？

科目：czsx 来源： 题型：

科目：czsx 来源：11.2三角形全等的判定同步练习数学卷 题型：填空题

科目：czsx 来源：2011-2012学年河北石家庄初中毕业班教学质量检测数学试卷（解析版） 题型：解答题

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

如图14所示，O为直线AB上一点，∠BOC=3∠AOC，OC平分∠AOD．

（1）求∠AOC的度数；

（2）推测OD与AB的位置关系，并说明理由．

 

科目：czsx 来源：新教材完全解读　九年级数学　(下册)　(配华东师大版新课标) 华东师大版新课标 题型：059

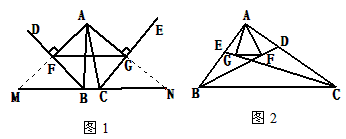
如图(1)所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连结FG，延长AF，AG，与直线BC相交，易证FG＝(AB＋BC＋AC)．

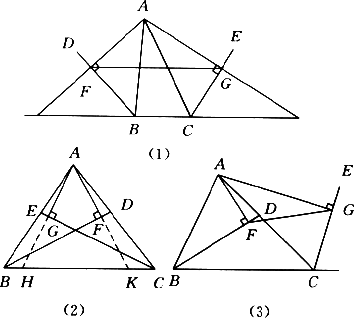
(1)若BD，CE分别是△ABC的内角平分线，如图(2)所示；

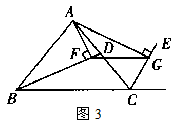
(2)BD为△ABC的内角平分线，CE为△ABC的外角平分线，如图(3)所示；

在图(2)、图(3)两种情况下，线段FG与△ABC的三边又有怎样的数量关系？请写出你的猜想，并对其中的一种情况给予证明．

科目：czsx 来源： 题型：

科目：czsx 来源：2006年初中数学总复习下册 题型：044

如图，小明家的一块四边形土地呈梯形ABCD的形状，其中AD∥BC，现在需要将这块土地平均分成两部分，种植两种作物进行对比实验，请你设计一种方案，仅用一条直线，将梯形ABCD的面积分成相等的两部分，现有两名同学小明和小刚的方法如下：

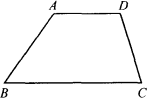
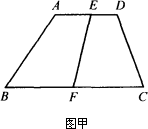
小明的方案：如图甲所示，分别取AD、BC的中点E、F，连结EF，则四边形ABFE与四边形DCFE的面积相等．

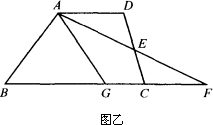
小刚的方案：如图乙所示．取DC的中点E，连结AE并延长交BC的延长线于点F，取BF的中点G连结AG，则△ABG与四边形AGCD的面积相等．

(1)你认为谁的方案正确？请说明你的理由．

(2)你还有其他方案，可平分梯形ABCD的面积吗？若有，请你画出示意图．

科目：czsx 来源：河北省模拟题 题型：解答题

（1）如图1所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连结FG，延长AF，AG，与直线BC分别交于点M、N，那么线段FG 与△ABC的周长之间存在的数量关系是什么？即：FG=____（AB+BC+AC）（直接写出结果即可）
（2）如图2，若BD，CE分别是△ABC的内角平分线；其他条件不变，线段FG与ΔABC三边之间又有怎样的数量关系？请写出你的猜想，并给予证明。
（3）如图3，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，其他条件不变，线段FG与ΔABC三边又有怎样的数量关系？直接写出你的猜想即可。不需要证明。

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

已知△ABC，
（1）如图1，若D点是△ABC内任一点，BD、CD分别为∠ABC、∠ACB的角平分线． 则∠D、∠A的关系为

∠D=90°+

1

2

∠A

∠D=90°+

1

2

∠A

．
（2）若D点是△ABC外一点，位置如图2所示．BD、CD分别为∠FBC、∠ECB的角平分线． 则∠D、∠A的关系为

∠D=90°-

1

2

∠A

∠D=90°-

1

2

∠A

．
（3）若D点是△ABC外一点，位置如图3所示．BD、CD分别为∠ABC、∠ECA的角平分线． 则∠D、∠A的关系为

∠D=

1

2

∠A

∠D=

1

2

∠A

．

科目：czsx 来源： 题型：

4、如图，已知：∠A=∠D，要使△ABC≌△DCB，只需增加一个条件是（　　）

A、AC=DB

B、BC=CB

C、∠ABC=∠DCB

D、AB=DC