精英家教网 >
试题搜索列表 >已知,∠aob=90°,om平分∠aob,将一块直角三角板的直角顶点p在射线om上移动,两直角边分别与边oa,ob交于点c,d,则线段pc与pd相等吗?为什么?
已知,∠aob=90°,om平分∠aob,将一块直角三角板的直角顶点p在射线om上移动,两直角边分别与边oa,ob交于点c,d,则线段pc与pd相等吗?为什么?答案解析
科目:czsx
来源:
题型:
(2013•鹰潭模拟)某校九年级(1)班数学兴趣小组开展了一次活动,过程如下:
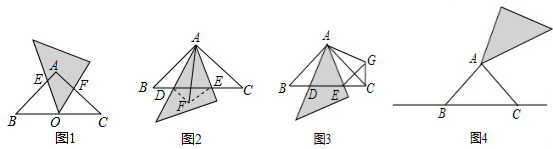
如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小明将一块直角三角板的直角顶点放在斜边BC边的中点O上,从BC边开始绕点A顺时针旋转,其中三角板两条直角边所在的直线分别交AB、AC于点E、F.
(1)小明在旋转中发现:在图1中,线段AE与CF相等.请你证明小明发现的结论;
(2)小明将一块三角板中含45°角的顶点放在点A上,从BC边开始绕点A顺时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.当0°<α≤45°时,小明在旋转中还发现线段BD、CE、DE之间存在如下等量关系:
BD
2+CE
2=DE
2.同组的小颖和小亮随后想出了两种不同的方法进行解决:
小颖的方法:将△ABD沿AD所在的直线对折得到△ADF,连接EF(如图2);
小亮的方法:将△ABD绕点A逆时针旋转90°得到△ACG,连接EG(如图3).
请你从中任选一种方法进行证明;
(3)小明继续旋转三角板,在探究中得出:当45°<α<135°且α≠90°时,等量关系BD
2+CE
2=DE
2仍然成立.现请你继续探究:当135°<α<180°时(如图4),等量关系BD
2+CE
2=DE
2是否仍然成立?若成立,给出证明;若不成立,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
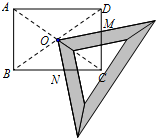
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
?若存在,请求出此时DM的长;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2007年江苏省无锡市崇安区中考数学一模试卷(解析版)
题型:解答题
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
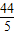
?若存在,请求出此时DM的长;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
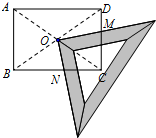 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于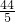 ?若存在,请求出此时DM的长;若不存在,请说明理由.
?若存在,请求出此时DM的长;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
操作:在△ABC中,AC=BC=4,∠C=90°,将一块直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况.
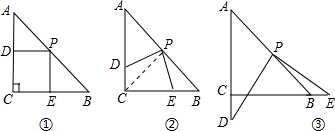
探究:(1)如图①,PD⊥AC于D,PE⊥BC于E,则重叠部分四边形DCEP的面积为
4
4
,周长
8
8
.
(2)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②加以证明.
(3)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•临沂)如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)当PE⊥AB,PF⊥BC时,如图1,则
的值为
;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,
的值是否变化?证明你的结论.

查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(山东临沂卷)数学(解析版)
题型:解答题
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
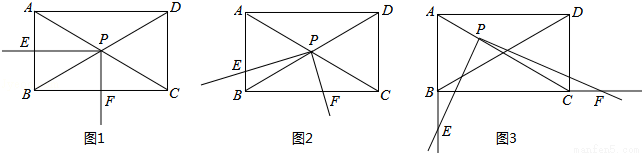
(1)当PE⊥AB,PF⊥BC时,如图1,则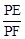 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求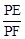 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,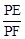 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:czsx
来源:2013年山东省临沂市高级中等学校招生考试数学
题型:044
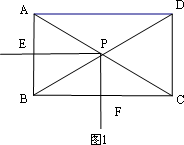
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为________.
的值为________.
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;

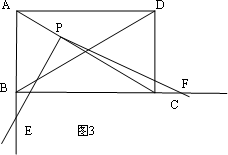
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP∶PC=1∶2时,如图3, 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:czsx
来源:2011-2012学年湖北省黄冈市浠水县朱店中学九年级(上)第二次月考数学试卷(解析版)
题型:解答题
操作:在△ABC中,AC=BC=4,∠C=90°,将一块直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况.

探究:(1)如图①,PD⊥AC于D,PE⊥BC于E,则重叠部分四边形DCEP的面积为______,周长______.
(2)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②加以证明.
(3)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD(AB<BC)的对角线交点O旋转(如图①→②→③),图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.
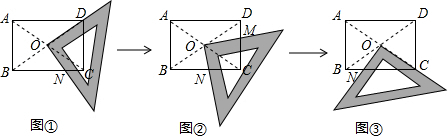
(1)该学习小组中一名成员意外地发现:在图①(三角板的一直角边与OD重合)中,BN
2=CD
2+CN
2;在图③(三角板的一直角边与OC重合)中,CN
2=BN
2+CD
2.请你对这名成员在图①和图③中发现的结论选择其一说明理由.
(2)试探究图②中BN、CN、CM、DM这四条线段之间的关系,写出你的结论,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
24、某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①⇒②⇒③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
(1)该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN
2=CD
2+CN
2,在图③中(三角板一边与OC重合),CN
2=BN
2+CD
2,请你对这名成员在图①和图③中发现的结论选择其一说明理由.
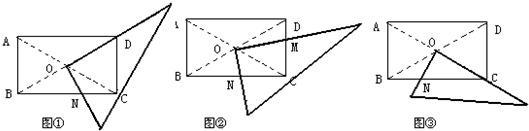
(2)试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由.
(3)将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之间所满足的数量关系.(不需要证明)

查看答案和解析>>
科目:czsx
来源:
题型:

如图所示,将一块直角三角板的直角顶点O放在直尺的一边CD上,如果∠AOC=28°,那么∠BOD等于( )
查看答案和解析>>
科目:czsx
来源:
题型:
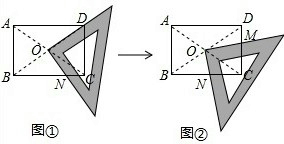
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD(DC<BC)的对角线交点O旋转(如图①→②),图中M、N分别为直角三角板的直角边与三角形DBC的边CD、BC的交点.
(1)在图①(三角板的一直角边与OD重合)中,有CN
2+DC
2=BN
2成立,请说明理由.
(2)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,请你用一个等式在横线上直接表示出探究的结论:
CN2+CM2=DM2+BN2
CN2+CM2=DM2+BN2
.证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,边长为1的正方形ABCD中,以A为圆心,1为半径作
,将一块直角三角板的直角顶点P放置在
(不包括端点B、D)上滑动,一条直角边通过顶点A,另一条直角边与边BC相交于点Q,连接PC,并设PQ=x,以下我们对
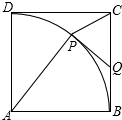
△CPQ进行研究.
(1)△CPQ能否为等边三角形?若能,则求出x的值;若不能,则说明理由;
(2)求△CPQ周长的最小值;
(3)当△CPQ分别为锐角三角形、直角三角形和钝角三角形时分别求x的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
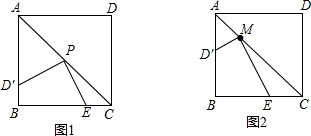
在正方形ABCD中,将一块直角三角板的直角顶点放在对角线AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别交线段AB、BC于D′、E两点.如图1是旋转三角板后所得到图形中的1种情况.
(1)三角板绕点P旋转,观察线段PF和PE之间有什么数量关系?并结合如图1加以证明;
(2)若将三角板的直角顶点放在对角线AC上的M处,且AM:MC=2:5,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合如图2加以证明.
查看答案和解析>>
科目:czsx
来源:2011-2012学年山东威海市八年级下期末模拟数学试卷(三)(带解析)
题型:解答题
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。

⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。

⑶将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系(不需要证明)
查看答案和解析>>
科目:czsx
来源:2013届山东威海市八年级下期末模拟数学试卷(三)(解析版)
题型:解答题
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。

⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。

⑶将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系(不需要证明)
查看答案和解析>>
科目:czsx
来源:
题型:
在正方形ABCD中,将一块直角三角板的直角顶点放在对角线AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别交线段AB、BC于D、E两点.如图1是旋转三角板后所得到图形中的1种情况.
(1)三角板绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合如图1加以证明.
(2)若将三角板的直角顶点放在对角线AC上的M处,且AM∶MC=2∶5,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合如图2加以证明.

查看答案和解析>>
科目:czsx
来源:2011-2012学年湖北省武汉市武昌区水果湖中学九年级(上)期中数学试卷(解析版)
题型:解答题
如图,边长为1的正方形ABCD中,以A为圆心,1为半径作
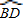
,将一块直角三角板的直角顶点P放置在

(不包括端点B、D)上滑动,一条直角边通过顶点A,另一条直角边与边BC相交于点Q,连接PC,并设PQ=x,以下我们对△CPQ进行研究.
(1)△CPQ能否为等边三角形?若能,则求出x的值;若不能,则说明理由;
(2)求△CPQ周长的最小值;
(3)当△CPQ分别为锐角三角形、直角三角形和钝角三角形时分别求x的取值范围.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD(AB<BC)的对角线交点O旋转(如图①→②→③),图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.

(1)该学习小组中一名成员意外地发现:在图①(三角板的一直角边与OD重合)中,BN
2=CD
2+CN
2;在图③(三角板的一直角边与OC重合)中,CN
2=BN
2+CD
2.请你对这名成员在图①和图③中发现的结论选择其一说明理由.
(2)试探究图②中BN、CN、CM、DM这四条线段之间的关系,写出你的结论,并说明理由.
查看答案和解析>>


 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于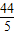 ?若存在,请求出此时DM的长;若不存在,请说明理由.
?若存在,请求出此时DM的长;若不存在,请说明理由.
 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于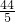 ?若存在,请求出此时DM的长;若不存在,请说明理由.
?若存在,请求出此时DM的长;若不存在,请说明理由.


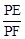 的值为 ;
的值为 ;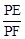 的值;
的值;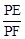 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.![]() 的值为________.
的值为________.
![]() 的值;
的值;
![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.








 △CPQ进行研究.
△CPQ进行研究.





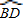 ,将一块直角三角板的直角顶点P放置在
,将一块直角三角板的直角顶点P放置在 (不包括端点B、D)上滑动,一条直角边通过顶点A,另一条直角边与边BC相交于点Q,连接PC,并设PQ=x,以下我们对△CPQ进行研究.
(不包括端点B、D)上滑动,一条直角边通过顶点A,另一条直角边与边BC相交于点Q,连接PC,并设PQ=x,以下我们对△CPQ进行研究.
