已知抛物线y=ax2+bx+c（a≠0）经过A（-2，0），B（0，-4），C（2，-4）三点，且与x轴的另一个交点为E． 若点P为抛物线第四象限部分一动点，求四边形ABPE的面积的最在值和此时点P的坐标。； ABDE的面积．答案解析

科目：czsx 来源： 题型：

（2013•泸州）如图，在直角坐标系中，点A的坐标为（-2，0），点B的坐标为（1，-

3

），已知抛物线y=ax²+bx+c（a≠0）经过三点A、B、O（O为原点）．
（1）求抛物线的解析式；
（2）在该抛物线的对称轴上，是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由；
（3）如果点P是该抛物线上x轴上方的一个动点，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．（注意：本题中的结果均保留根号）

科目：czsx 来源： 题型：

已知抛物线y=ax²+bx+c（a≠0）经过A（-2，0）、B（0，1）两点，且对称轴是y轴．经过点C（0，2）的直线l与x轴平行，O为坐标原点，P、Q为抛物线y=ax²+bx+c（a≠0）上的两动点．
（1）求抛物线的解析式；
（2）以点P为圆心，PO为半径的圆记为⊙P，判断直线l与⊙P的位置关系，并证明你的结论；
（3）设线段PQ=9，G是PQ的中点，求点G到直线l距离的最小值．

科目：czsx 来源： 题型：

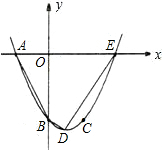
如图，已知抛物线y=ax²+bx+c（a≠0）经过A（-2，0），B（0，-4），C（2，-4）三点，且与x轴的另一个交点为E．
（1）求抛物线的解析式；
（2）用配方法求抛物线的顶点D的坐标和对称轴；
（3）求四边形ABDE的面积．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

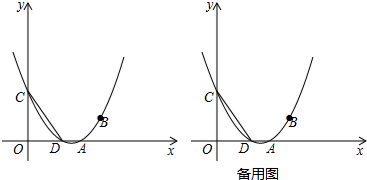
（2013•鞍山二模）已知抛物线y=ax²+bx+3（a≠0）经过A（3，0），B（4，1）两点，与x轴另一交点为D，与y轴交于点C．
（1）求抛物线y=ax²+bx+3（a≠0）的函数关系式；
（2）如图，连接AC，在抛物线上是否存在点P，使∠ACD+∠ACP=45°？若存在，求出点P的坐标；若不存在，请说明理由；
（3）连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F，
①点E在运动过程中四边形OEAF的面积是否发生变化，并说明理由；
②当EF分四边形OEAF的面积为1：2两部分时，求点E的坐标．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

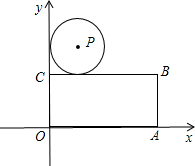
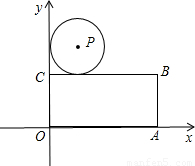
如图，在平面直角坐标系中，矩形OABC的顶点A的坐标为（4，0），点C的坐标为（0，2），O为坐标原点．设P点在第一象限，以P为圆心，半径为1的⊙P与y轴及矩形OABC的边BC都相切．已知抛物线y=ax²+bx+c（a≠0）经过O、P、A三点．
（1）求抛物线的解析式；
（2）若⊙P与矩形OABC组合得到的图形的面积能被一条直线l平分，求这条直线l的解析式；
（3）若点N在抛物线上，问x轴上是否存在点M，使得以M为圆心的⊙M能与△PAN的三边PA、PN、AN所在直线都相切？若存在，请求出M点的坐标；若不存在，请说明理由．

科目：czsx 来源： 题型：

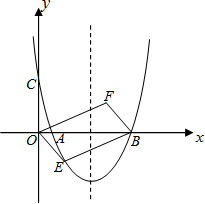
（2012•利川市二模）如图，已知抛物线y=ax²+bx+c（a≠0）经过A（-4，3）、B（2，0）两点，对称轴为y轴，经过点C（0，-2）的直线l与x轴平行，P（m，n）是抛物线上的动点，O为坐标原点．
（1）求直线AB和抛物线的函数解析式；
（2）以A为圆心，AO为半径画⊙A，判断直线l与⊙A的位置关系，并说明理由；
（3）设PO=d₁，点P到直线l的距离为d₂，试探索d₁、d₂间的数量关系；
（4）D点在直线AB上，D点的横坐标为-2，当△PDO的周长最小时，求四边形CODP的面积．

科目：czsx 来源： 题型：

如图，已知抛物线y=ax²+bx+c（a≠0）经过点A（1，0），B（6，0）和C（0，4 ）三个点．
（1）求抛物线的解析式；
（2）设点E（m，n）是抛物线上一个动点，且位于第四象限，四边形OEBF是以OB为对角线的平行四边形，求四边形OEBF的面积S与m之间的函数关系式，并写出自变量m的取值范围；
（3）当四边形OEBF的面积为24时，请判断四边形OEBF是否为菱形？

科目：czsx 来源： 题型：

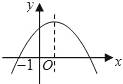
已知抛物线y=ax²+bx+c（a≠0）经过点（-1，0），且顶点在第一象限．有下列三个结论：①a＜0；②a+b+c＞0；③-

b

2a

＞0．把正确结论的序号填在横线上

 

．

科目：czsx 来源： 题型：

（2012•安溪县质检）如图，已知抛物线y=ax²+bx+c（a≠0）经过A（-1，0）、B（3，0）、C（0，-

3

2

）．
（1）求该抛物线的解析式；
（2）若点Q在抛物线的对称轴上，点P在抛物线上，若以O、B、P、Q为顶点的四边形是平行四边形，求所有满足条件的点P的坐标；
（3）请在抛物线对称轴上求点M，使得∠BMC=90°．

科目：czsx 来源： 题型：

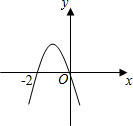
如图所示，已知抛物线y=ax²+bx+c（a≠0）经过原点和点（-2，0），则2a-3b

 

0．（＞、＜或=）

科目：czsx 来源： 题型：

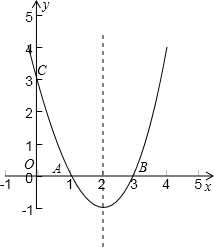
已知抛物线y=ax²+bx+c（a≠0）经过点B（2，0）和点C（0，8），且它的对称轴是直线x=-2．
（1）求抛物线与x轴的另一交点A的坐标；
（2）求此抛物线的解析式；
（3）连接AC，BC，若点E是线段AB上的一个动点（与点A，点B）不重合，过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式；
（4）在（3）的基础上试说明S是否存在最大值？若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

科目：czsx 来源： 题型：

如图，已知抛物线y=ax²+bx+c（a≠0）经过点A（1，0）、B（3，0）、C（0，3）．
（1）试求出抛物线的解析式；
（2）问：在抛物线的对称轴上是否存在一个点Q，使得△QAC的周长最小，试求出△QAC的周长的最小值，并求出点Q的坐标；
（3）现有一个动点P从抛物线的顶点T出发，在对称轴上以1个单位长度每秒的速度向y轴的正方向运动，试问，经过几秒后，△PAC是等腰三角形？

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

（2013•本溪一模）如图，已知抛物线y=ax²+bx+3（a≠0）经过A（-1，0），C（3，0）两点．
（1）求抛物线的解析式；
（2）如图，动点D从点O开始沿OB向终点B以每秒1个单位长度的速度运动，动点E从点O开始沿OC向终点C以每秒2个单位长度的速度运动，过点E作GE⊥OC，交CB于点F，交抛物线y=ax²+bx+3于点G，连接BG，DF，点D，E从点O同时出发，当其中一点到达端点时，另一点也随之停止运动．设运动时间为t秒（t≥0），在运动过程中，若四边形BDFG为正方形，求t的值；
（3）将（2）中的正方形BDFG沿y轴翻折180°，得到正方形BDF′G′，然后将正方形BDF′G′沿直线BC方向向下平移，设在平移过程中正方形BDF′G′与△BOC重合部分的面积为S，平移的距离为m（0≤m≤3

2

），请直接写出S与m之间的函数关系式．

科目：czsx 来源： 题型：

已知抛物线y=ax²+bx+3（a≠0）经过A（3，0），B（4，1）两点，且与y轴交于点C．
（1）求抛物线y=ax²+bx+3（a≠0）的函数关系式及点C的坐标；
（2）如图（1），连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；
（3）如图（2），连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F，当△OEF的面积取得最小值时，求点E的坐标．

科目：czsx 来源： 题型：

科目：czsx 来源：2007年湖北省武汉市黄陂一中分配生素质测试数学试卷（解析版） 题型：解答题

如图，在平面直角坐标系中，矩形OABC的顶点A的坐标为（4，0），点C的坐标为（0，2），O为坐标原点．设P点在第一象限，以P为圆心，半径为1的⊙P与y轴及矩形OABC的边BC都相切．已知抛物线y=ax²+bx+c（a≠0）经过O、P、A三点．
（1）求抛物线的解析式；
（2）若⊙P与矩形OABC组合得到的图形的面积能被一条直线l平分，求这条直线l的解析式；
（3）若点N在抛物线上，问x轴上是否存在点M，使得以M为圆心的⊙M能与△PAN的三边PA、PN、AN所在直线都相切？若存在，请求出M点的坐标；若不存在，请说明理由．