科目：gzsx 来源： 题型：
| 1 |
| 3 |
| 1 |
| 2 |
科目：gzsx 来源：新课标教材全解高中数学人教A版必修1 人教A版 题型：022
设某物体在8∶00和16∶00之间的温度T是时间t的函数：T(t)＝at2＋bt＋c(a≠0)，其中温度的单位是℃，时间的单位是小时，t＝0表示12∶00，t取正值表示12∶00以后，若测得该物体在8∶00的温度为8℃，12∶00的温度为60℃，13∶00的温度为58℃，则T(t)＝________．
科目：gzsx 来源： 题型：
.有一个数据为50的样本，数据分组的频数如下:［12.5,15.5) 3,［15.5,18.5) 8,［18.5,21.5) 9,［21.5,24.5) 11,［24.5,27.5) 10,［27.5,30.5) 5,［30.5,33.5) 4.根据频率分布，估计在［18.5,27.5)之间的数据大约占
A.60% B.92% C.5% D.65%
科目：gzsx 来源： 题型：
A.60% B.92% C.5% D.65%
科目：gzsx 来源：2014届甘肃省高二第二次月考理科数学试卷（解析版） 题型：解答题
（本小题满分12分）设某物体一天中的温度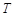
是时间
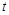的函数：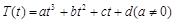
，其中温度的单位是
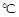，时间单位是小时，
表示12:00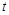，取正值表示12:00以后．若测得该物体在8:00的温度是
，12:00的温度为
，13:00的温度为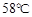
，且已知该物体的温度在8:00和16:00有相同的变化率．
（1）写出该物体的温度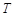关于时间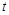的函数关系式；
（2）该物体在10:00到14:00这段时间中（包括10:00和14:00），何时温度最高，并求出最高温度；
（3）如果规定一个函数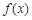
在区间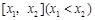
上的平均值为
，求该物体在8:00到16:00这段时间内的平均温度．
科目：gzsx 来源： 题型：
(1)求f(x)的表达式和极值.
(2)若f(x)在区间［m,m+4］上是单调函数,试求m的取值范围.
(3)存在正数t,使得对任意x1,x2∈［-t,t］,|f(x1)-f(x2)|≤27恒成立,试求t的取值范围.
科目：gzsx 来源： 题型：
(12分) 在数学必修(3)模块修习测试中,某校有1000名学生参加,从参加考试的学生中抽出60名,将其考试成绩(均为整数)整理后画出的频率分布直方图如下,试根据图形提供的信息解答下列问题.
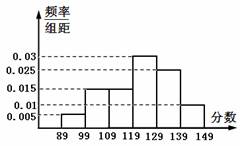(1)求出这60名学生的考试成绩众数的估计值;
(2)分别求出成绩在[89,99)和[99,109)之间的人数;
(3)若成绩在[89,99)中有2人没及格(90分以及以上为及格),
求成绩在[89,109)之间的所有学生中随机抽取2人,至
少有1人没及格的概率.
科目：gzsx 来源： 题型：
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
科目：gzsx 来源： 题型：
科目：gzsx 来源： 题型：
科目：gzsx 来源： 题型：
| 51 | 25 |
科目：gzsx 来源： 题型：
科目：gzsx 来源： 题型：
|
| A、f（x）在x=1处不连续 |
| B、f（x）在x=2处不连续 |
| C、f（x）在x=1和x=2处不连续 |
| D、f（x）处处连续 |
科目：gzsx 来源： 题型：
科目：gzsx 来源： 题型：
科目：gzsx 来源： 题型：
|
科目：gzsx 来源：2013届广东省梅州市高二第二学期3月月考理科数学试卷 题型：解答题
已知函数f（x）=2x3+ax2+bx+3在x=-1和x=2处取得极值．
（1）求f（x）的表达式和极值．
（2）若f（x）在区间[m，m+4]上是单调函数，试求m的取值范围．（14分）
在x=-3和x=2处取得极值，问：当c为何值时，不等式ax2+bx+c≤0在[1，4]上恒成立？
在区间[a，a+3]上的值
出现的次数不小于4次，又不多于8次，则k可以取