练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >第一象限内的点p（x，y）为直线y=-2x+4上的一个动点，pa垂直x轴，pb垂直y轴，垂直分别是a，b

    第一象限内的点p（x，y）为直线y=-2x+4上的一个动点，pa垂直x轴，pb垂直y轴，垂直分别是a，b答案解析

    科目：gzsx 来源： 题型：

    设P为双曲线C：
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的渐近线在第一象限内的部分上一动点，F为双曲线C的右焦点，A为双曲线C的右准线与x轴的交点，e是双曲线C的离心率，则∠APF的余弦的最小值为（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设点P为直线y=
    b
    2a
    x    与椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞c＞0)    在第一象限内的交点，点F是椭圆的右焦点，若PF垂直于x轴，则椭圆的离心率e=
    2
    		5
    5
    2
    		5
    5
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的右焦点与抛物线C2：y2=4x的焦点F重合，点M是C1与C2在第一象限内的交点，且|MF|=
    5
    3
    ．
    （1）求椭圆C1的方程；
    （2）设抛物线的准线与x轴交于点E，过E任作一条直线l，l与椭圆C1的两个交点记为A，B．问：在椭圆的长轴上是否存在一点P，使
    PA
    •
    PB
    为定值？若存在，求出点P的坐标及相应的定值；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设P为双曲线C：
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的渐近线在第一象限内的部分上一动点，F为双曲线C的右焦点，A为双曲线C的右准线与x轴的焦点，若∠APF的最大值为
    π
    3
    ，则双曲线的离心率为
    2
    2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

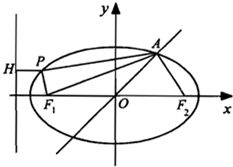
    精英家教网已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的短轴长为4，F1F2分别是椭圆C的左，右焦点，直线y=x与椭圆C在第一象限内的交点为A，△AF1F2的面积为2
    		6
    ，点P（x0，y0），是椭圆C上的动点w．
    （1）求椭圆C的方程；
    （2）若∠F1PF2为钝角，求点P的横坐标x0的取值范围；
    （3）求
    		3
    PF1+
    		2
    PA的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C中心在原点，焦点在坐标轴上，直线y=
    3
    2
    x    与椭圆C在第一象限内的交点是M，点M在x轴上的射影恰好是椭圆C的右焦点F2，椭圆C另一个焦点是F1，且
    MF1
    •
    MF2
    =
    9
    4
    ．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）直线l过点（-1，0），且与椭圆C交于P，Q两点，求△F2PQ的内切圆面积的最大值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    直线y=-
    		3
    3
    x+1    与x轴，y轴分别交于点A，B，以线段AB为边在第一象限内作等边△ABC，如果在第一象限内有一点P(m，
    1
    2
    )    ，使得△ABP和△ABC面积相等，则m的值（　　）
    A、
    5
    		3
    2
    B、
    3
    		3
    2
    C、
    		3
    2
    D、
    		3

    查看答案和解析>>

    科目：gzsx 来源： 题型：

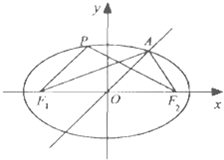
    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的短轴长为4，F1，F2分别是椭圆C的左，右焦点，直线y=x与椭圆C在第一象限内的交点为A，△AF1F2的面积为2
    		6
    ，点P（x0，y0）是椭圆C上的动点
    （1）求椭圆C的方程
    （2）若∠F1PF2为钝角，求点P的横坐标x0的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•安徽）设椭圆E：
    x2
    a2
    +
    y2
    1-a2
    =1    的焦点在x轴上
    （1）若椭圆E的焦距为1，求椭圆E的方程；
    （2）设F1，F2分别是椭圆E的左、右焦点，P为椭圆E上第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q，证明：当a变化时，点P在某定直线上．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设点P是抛物线C：x2=2py（p＞0）在第一象限内的任意一点，过P作抛物线C的切线l交x轴于点M，F为抛物线C的焦点，点Q满足
    PM
    =
    1
    2
    PF
    +
    1
    2
    PQ
    ，若△PFQ是面积为
    		3
    的等边三角形，则p的值为
    1
    1
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图，双曲线C1：
    x2
    4
    -
    y2
    b2
    =1    与椭圆C2：
    x2
    4
    +
    y2
    b2
    =1    （0＜b＜2）的左、右顶点分别为A1、A2第一象限内的点P在双曲线C1上，线段OP与椭圆C2交于点A，O为坐标原点．
    （I）求证：
    kAA1+kAA2
    kPA1+kPA2
    为定值（其中kAA1表示直线AA1的斜率，kAA2等意义类似）；
    （II）证明：△OAA2与△OA2P不相似．
    （III）设满足{（x，y）|
    x2
    4
    -
    y2
    m2
    =1    ，x∈R，y∈R}⊆{（x，y）|
    x2
    4
    -
    y2
    3
    ＞1    ，x∈R，y∈R} 的正数m的最大值是b，求b的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知第一象限内的点M到x轴、y轴的距离分别为5、4，点N的坐标是（0，3），经过点M、N的圆P的圆心P在x轴上．
    （1）求圆P的方程   
    （2）若点Q（x，y）在圆P上，求：3x+4y的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

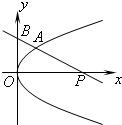
    精英家教网如图，设点A（x0，y0）为抛物线y2=
    x2
    上位于第一象限内的一动点，点B（0，y1）在y轴正半轴上，且|OA|=|OB|，直线AB交x轴于点P（x2，0）．
    （Ⅰ）试用x0表示y1；
    （Ⅱ）试用x0表示x2；
    （Ⅲ）当点A沿抛物线无限趋近于原点O时，求点P的极限坐标．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    直线y=-
    		3
    3
    x+1    和x轴，y轴分别交于点A，B，在线段AB为边在第一象限内作等边△ABC，如果在第一象限内有一点P(m，
    1
    2
    )    使得△ABP和△ABC的面积相等，求m的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知直线y=-x+1与椭圆
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）相交于A、B两点，且OA⊥OB（其中O为坐标原点）．
    （1）若椭圆的离心率为
    1
    2
    ，求椭圆的方程；
    （2）求证：不论a，b如何变化，椭圆恒过第一象限内的一个定点P，并求点P的坐标．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知直线x+y=1经过第一象限内的点P(
    1
    a
    ，
    1
    b
    )，则a+4b    的最小值为
    9
    9
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网函数y=f（x），x∈[-5，5]的图象如图所示，该曲线在原点处的切线的方程为y=x，且导函数f′（x）是减函数．给出下列四个命题：
    ①A，B是该图象上的任意两点，那么直线AB的斜率kAB∈（0，1）；
    ②点P是该图象在第一象限内的部分上的点，那么直线OP的斜率kOP∈（0，1）；
    ③对于∀x1，x2∈[-5，5]，f（x1）+f（x2）≤2f（
    x1+x2
    2
    ）恒成立；
    ④对于∀x∈[-5，5]，f（x）≤x．
    其中所有真命题的序号是（　　）
    A、①②③B、②③④
    C、②④D、①③

    查看答案和解析>>

    科目：gzsx 来源： 题型：

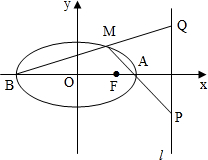
    精英家教网如图，点A、B为椭圆
    x2
    4
    +
    y2
    2
    =1    长轴的两个端点，点M为该椭圆上位于第一象限内的任意一点，直线AM、BM分别与直线l：x=2
    		2
    相交于点P、Q．
    （1）若点P、Q关于x轴对称，求点M的坐标；
    （2）证明：椭圆右焦点F在以线段PQ为直径的圆上．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    有定点P（6，4）及定直线l：y=4x，Q是l上在第一象限内的点．PQ交x轴的正半轴于M点，问点Q在什么位置时，△OMQ的面积最小，并求出最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点P在第一象限内，以P为圆心的圆过点A（-1，2）和B（1，4），线段AB的垂直平分线交圆P于C、D两点，且|CD|=2
    		10
    ．
    （1）求直线CD的方程；
    （2）求圆P的方程；
    （3）若直线AB与x轴交于点M，求
    MC
    •
    MD
    的值．

    查看答案和解析>>