科目：czsx 来源： 题型：
如图，在△ABC中，∠C=90°，AD平分∠ABC，交BC于D点，作DE⊥AB于点E，若△ADC与△ABC的面积之比为3：7，则△BED与△AED的面积之比为科目：czsx 来源： 题型：
3、如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，则下列结论：①AD平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④BE+AC=AB，其中正确的有（ ）科目：czsx 来源： 题型：
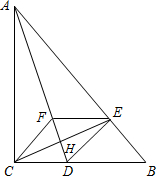（2012•鼓楼区二模）已知：如图，在△ABC中，∠ACB=90°，AD平分∠CAB，DE⊥AB，垂足为E，CD=ED．连接CE，交AD于点H． 科目：czsx 来源： 题型：
（2013•温州）如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．
12、如图，在△ABC中，∠C=90°，AD平分∠BAC，若CD=6 cm，则点D到AB的距离是
14、如图，在△ABC中，∠BAC=90°，AD⊥BC，则图中互为余角的有
15、如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB，若∠BAD=30°，CB=6，则∠B=
16、如图，在△ABC中，∠C=90°，AD是△ABC中∠CAB的角平分线，DE⊥AB于E，BD=5，BC=8，则DE=
13、如图，在△ABC中，∠C=90°，AD平分∠CAB，BC=6，BD=4，则点D到AB的距离是
如图：在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F．
（1997•广州）如图，在△ABC中，∠BAC=90°，AD⊥BC，垂足为D，DE⊥AB，垂足为E，则图中与△ADE相似的三角形的个数为（ ）
33、如图，在△ABC中，∠C=90°，AD平分∠CAB，BC=8cm，BD=5cm，那么D点到直线AB的距离是
22、如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB，垂足为E，BC=6，DE=2，则DB=
如图，在△ABC中，∠ACB=90°，AD是△ABC的角平分线，BC=10cm，BD：DC=3：2，则点D到AB的距离为
5、如图，在△ABC中，∠ACB=90°，AD=AC，BE=BC，则∠DCE的大小为（ ）
如图，在△ABC中，∠ACB=90°，AD平分∠BAC，BC=9，BD=5，则点D到AB的距离为（ ）
25、如图，在△ABC中，∠ACB=90°，AD是角平分线，CH是高，交AD于F，DE⊥AB于E，试证明四边形CDEF是菱形．
如图，在△ABC中，∠B=90°，AD是∠BAC的角平分线，交BC于D，过D作AC的垂线交AC于E．若E正好是AC的中点，则∠C=
如图，在△ABC中，∠BAC=90°，AD⊥BC于点D，AE平分∠DAC，∠B=50°，
2、如图，在△ABC中，∠BAC=90°，AD⊥BC，垂足为D，DE⊥AB，垂足为E，则图中与△ADE相似的三角形个数为（ ）