
科目:gzsx 来源: 题型:
| ax+1+bx+1 |
| ax+bx |
| a2+b2 |
| a+b |
| ab |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源:2008-2009学年江苏省苏州市(五市三区)高二(下)期末数学试卷(文科)(解析版) 题型:解答题
科目:gzsx 来源:不详 题型:解答题
科目:gzsx 来源:2008-2009学年江苏省苏州市(五市三区)高二(下)期末数学试卷(理科)(解析版) 题型:解答题
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源:不详 题型:解答题
| ax+1+bx+1 |
| ax+bx |
| a2+b2 |
| a+b |
| ab |
科目:gzsx 来源:福建省福州三中2012届高三第二次月考数学理科试题 题型:044
已知a,b∈R,函数f(x)=ln(x+1)-x2+ax+b的图象经过点A(0,2).
(1)若曲线y=f(x)在点A处的切线与直线3x-y-1=0平行,求实数a的值;
(2)若函数f(x)在[1,+∞)上为减函数,求实数a的取值范围;
(3)令a=-1,c∈R,函数g(x)=c+2cx-x2,若对任意x1∈(-1,+∞),总存在x2∈[-1,+∞),使得f(x1)=g(x2)成立,求实数c的取值范围.
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源: 题型:
| 1 | ||
|
科目:gzsx 来源: 题型:
 已知m,t∈R,函数f (x)=(x-t)3+m.
已知m,t∈R,函数f (x)=(x-t)3+m.科目:gzsx 来源: 题型:
| 1 | ||
|
科目:gzsx 来源:2010-2011学年吉林省高三第一次模拟考试数学理卷 题型:选择题
已知:定义域为R的函数f(x)为奇函数,当x>0时,f(x)= x3 +1;则x<0时,f(x)的解析式为
A f(x)= x3 +1 B f(x)= x3 -1 C f(x)= -x3 +1 D f(x)= -x3 -1
科目:gzsx 来源:2011-2012学年福建省福州市高三第一学期期末质量检测文科数学 题型:解答题
(本小题满分1 4分)已知m,t∈R,函数f (x) =(x - t)3+m.
(I)当t =1时,
(i)若f (1) =1,求函数f (x)的单调区间;
(ii)若关于x的不等式f (x)≥x3—1在区间[1,2]上有解,求m的取值范围;
(Ⅱ)已知曲线y= f (x)在其图象上的两点A(x1,f (x1)),B(x2,f (x2)))( x1≠x2)处的切线
分别为l1、l2.若直线l1与l2平行,试探究点A与点B的关系,并证明你的结论.
科目:gzsx 来源:2011-2012学年江苏省高三上学期期中考试数学 题型:填空题
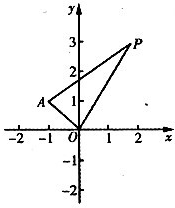
(文科)设向量 =(cos23°,cos67°),
=(cos23°,cos67°), =(cos68°,cos22°),
=(cos68°,cos22°), =
= +t
+t
(t∈R),则| |的最小值是____________
|的最小值是____________
(理科)已知a>0,设函数f(x)=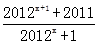 +sinx,x∈[-a,a]的最大值
+sinx,x∈[-a,a]的最大值
为M,最小值为m,则M+m=__________
科目:gzsx 来源:2012年宁夏高考数学仿真模拟试卷3(文科)(解析版) 题型:选择题