练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知an前n项和Sn=1+1/4an，求an

    已知an前n项和Sn=1+1/4an，求an答案解析

    科目：gzsx 来源：数学教研室 题型：044

    已知的前n项和Sn=1+kan(k≠1、0，常数)。

    (1)用n，k写出an的表达式；

    (2)若，求k的取值范围。

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在数列{an}中，已知其前n项和sn=2n+3，则an=
    5，n=1
    2n-1，n≥2
    5，n=1
    2n-1，n≥2
    ．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：填空题

    在数列{an}中，已知其前n项和sn=2n+3，则an=______．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知等差数列前n项和Sn=n2-17n,则使Sn最小的n值是（    ）

    A.8                B.9                 C.10                 D.8或9

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知等差数列前n项和Sn=n2-17n,则使Sn最小的n值是（    ）

    A.8                B.9                 C.10                 D.8或9

    查看答案和解析>>

    科目：gzsx 来源：数学教研室 题型：013

    已知的前n项和Sn和Tn，若，则等于（    ）

    A.1

    B.

    C.

    D.

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：013

    已知的前n项和Sn和Tn，若，则等于（    ）

    A.1

    B.

    C.

    D.

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    公差不为零的等差数列{an}中，已知其前n项和为Sn，若S8=S5+45，且a4，a7，a12成等比数列
    （Ⅰ）求数列{an}的通项an
    （Ⅱ）当bn=
    1Sn
    时，求数列{bn}的前n和Tn．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知分别以d1，d2为公差的等差数列{an}，{bn}满足a1=18，b14=36．
    （1）若d1=18，且存在正整数m，使得am2=bm+14-45，求证：d2＞108；
    （2）若ak=bk=0，且数列a1，a2，…，ak，bk+1，bk+2，…，b14的前n项和Sn满足S14=2Sk，求数列{an}，{bn}的通项公式；
    （3）在（2）的条件下，令cn=2an，dn=2bn，问不等式cndn+1≤cn+dn是否对n∈N*恒成立？请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知等差数列{an}的首项为a，公差为b，且不等式log2（ax2-3x+6）＞2的解集为{x|x＜1或x＞b}．
    （Ⅰ）求数列{an}的通项公式及前n项和Sn公式；
    （Ⅱ）求数列{
    1an•an+1
    }的前n项和Tn．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知分别以d1和d2为公差的等差数列和满足a1=18，b14=36．
    （1）若d1=18，且存在正整数m，使得am2=bm+14-45，求证：d2＞108；
    （2）若ak=bk=0，且数列a1，a2，…，ak，bk+1，bk+2，…，b14的前n项和Sn满足S14=2Sk，求数列{an}和{bn}的通项公式．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （Ⅰ）已知数列{an}的前n项和Sn=n2-2n+2，求通项公式an；
    （Ⅱ）已知等比数列{an}中，a3=
    3
    2
    ，S3=
    9
    2
    ，求通项公式an．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=x2+ax+b（a、b为实常数），已知不等式|f（x）|≤|2x2+4x-6|对任意的实数x均成立．定义数列{an}和{bn}：a1=3，2an=f（an-1）+3（n=2，3，…），bn=
    1
    2+an
    (n=1，2，…)    ，数列{bn}的前n项和Sn．
    （I）求a、b的值；
    （II）求证：Sn＜
    1
    3
    (n∈N*)    ；
    （III ）求证：an＞22n-1-1(n∈N*).

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知一个等差数列{an}前10项的和是
    125
    7
    ，前20项的和是-
    250
    7

    （1）求这个等差数列的前n项和Sn．
    （2）求使得Sn最大的序号n的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=alog2x，且关于x的方程
    a
    f(x)
    +2=
    f(x)
    a2
    有两个相同的实数解，数列{an}的前n项和sn=1+f（n+1），n∈N*
    （1）求数列{an}的通项公式；
    （2）试确定数列{an}中n的最小值m，使数列{an}从第m项起为递增数列；
    （3）设数列bn=1-an，一位同学利用数列{bn}设计了一个程序，其框图如图所示，但小明同学认为
    这个程序如果执行将会是一个“死循环”（即一般情况下，程序将会永远循环下去而无法结束）．
    你是否赞同小明同学的观点？请说明你的理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知分别以d1和d2为公差的等差数列{an}和{bn}满足a1=18，b14=36，
    （1）若d1=18，d2≥2917，且am2=bm+14-45，求m的取值范围；
    （2）若ak=bk=0，且数列a1，a2，…，ak，bk+1，bk+1，…，b14…的前n项和Sn满足S14=2Sk，
    ①求数列{an}和{bn}的通项公式；
    ②令An=aan，Bn=abn，a＞0且a≠1，探究不等式AnBn+1＜An+Bn是否对一切正整数n恒成立？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•门头沟区一模）已知等差数列{an}中，a2+a4=10，a5=9，数列{bn}中，b1=a1，bn+1=bn+an．
    （ I）求数列{an}的通项公式，写出它的前n项和Sn；
    （ II）求数列{bn}的通项公式；
    （ III）若cn=
    2an•an+1
    ，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知{an}是等比数列,a1=2,a4=54,{bn}是等差数列,b1=2,b1+b2+b3+b4=a1+a2+a3.

    (1)求数列{an}的通项公式及前n项和Sn的公式；

    (2)求数列{bn}的通项公式；

    (3)设Un=b1+b4+b7+…+b3n-2(其中n=1,2,…),求U10的值.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    ３已知等差数列{an},公差d大于0,且的两个根,数列{bn}的前n项和为Tn,且.

    （1）求数列{an}的前n项和Sn；

    （2）求{bn}的通项公式.

    查看答案和解析>>

    科目：gzsx 来源：2010年甘肃省高二下学期期末考试数学卷 题型：解答题

    （本小题满分12分）

     (理科)已知数列 {2 n•an} 的前 n 项和 Sn = 9－6n.

     (I)    求数列 {an} 的通项公式；

    (II)    设 bn = n·(2－log 2 )，求数列 { } 的前 n 项和Tn.

    （文科）已知，且f(0)=8及f(x+1)－f(x)＝－2x+1。

     (1)求的解析式；

     (2)求函数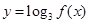的单调递减区间及值域．

     

    查看答案和解析>>