精英家教网 >
试题搜索列表 >解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D,如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系
解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D,如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系答案解析
科目:czsx
来源:
题型:阅读理解

24、先阅读下面的材料,然后解答问题:
已知:如图1等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.
求证:AC=AB+BD.
证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
我们将这种证明一条线段等于另两线段和的方法称为“截长法”.
解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D,如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
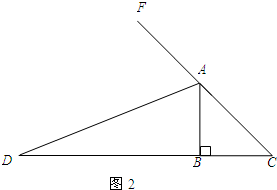
查看答案和解析>>
科目:czsx
来源:2011年河北省保定市中考数学一模试卷(解析版)
题型:解答题
先阅读下面的材料,然后解答问题:
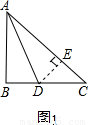
已知:如图1等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.
求证:AC=AB+BD.
证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
我们将这种证明一条线段等于另两线段和的方法称为“截长法”.
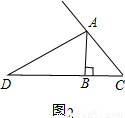
解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D,如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 先阅读下面的材料,然后解答问题:
先阅读下面的材料,然后解答问题:
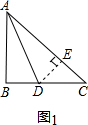
已知:如图1等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.
求证:AC=AB+BD.
证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
我们将这种证明一条线段等于另两线段和的方法称为“截长法”.
解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D,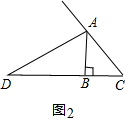 如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
【阅读理解】
已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.求证:AC=AB+BD证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
【解决问题】
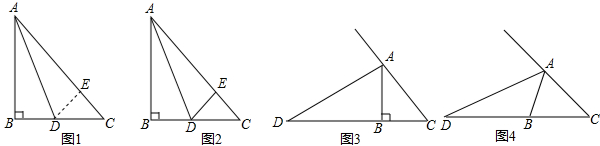
已知,如图2,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的平分线,交BC边于点D,DE⊥AC,垂足为E,若AB=2,则三角形DEC的周长为________.
【数学思考】:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D如图3”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
【类比猜想】
任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图4,请你写出线段AC、AB、BD之间的数量关系.
查看答案和解析>>
科目:czsx
来源:
题型:
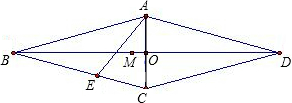
如图,在边长为1的菱形ABCD中,∠B=36°,对角线BD、AC相交于点O,∠BAC的平分线AE交BC边于点E.试解答下列几个问题:
(1)不用计算器求:①AE长度的准确值,②∠ABO正弦的准确值;
(2)在对角线BD上取一点M.求BM<AB的概率(如果计算的概率值为无理数,则将计算结果精确到百分位)
查看答案和解析>>
科目:czsx
来源:2012届河南安阳九年级5月中考模拟考试数学试卷(带解析)
题型:解答题
查看答案和解析>>
科目:czsx
来源:
题型:
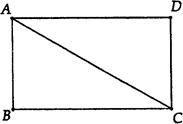
如图,在矩形ABCD中,

【小题1】请完成如下操作:①作

的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
【小题2】请在(1)的基础上,完成下列问题:
①判断直线BC与圆

的位置关系,并说明理由;
②若圆

与AC边的另一个交点为F,

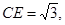
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
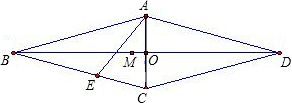
如图,在边长为1的菱形ABCD中,∠B=36°,对角线BD、AC相交于点O,∠BAC的平分线AE交BC边于点E.试解答下列几个问题:
(1)不用计算器求:①AE长度的准确值,②∠ABO正弦的准确值;
(2)在对角线BD上取一点M.求BM<AB的概率(如果计算的概率值为无理数,则将计算结果精确到百分位)
查看答案和解析>>
科目:czsx
来源:2009-2010学年北京课改版九年级(上)期末数学试卷1(解析版)
题型:解答题
如图,在边长为1的菱形ABCD中,∠B=36°,对角线BD、AC相交于点O,∠BAC的平分线AE交BC边于点E.试解答下列几个问题:
(1)不用计算器求:①AE长度的准确值,②∠ABO正弦的准确值;
(2)在对角线BD上取一点M.求BM<AB的概率(如果计算的概率值为无理数,则将计算结果精确到百分位)

查看答案和解析>>
科目:czsx
来源:
题型:
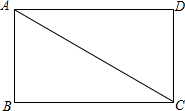
如图,在矩形ABCD中,AD>AB.
(1)请完成如下操作:①作∠BAC的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
(2)请在(1)的基础上,完成下列问题:
①判断直线BC与圆O的位置关系,并说明理由;
②若圆O与AC边的另一个交点为F,AC=3,CE=
,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在矩形ABCD中,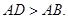
1.请完成如下操作:①作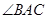 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
2.请在(1)的基础上,完成下列问题:
①判断直线BC与圆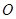 的位置关系,并说明理由;
的位置关系,并说明理由;
②若圆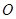 与AC边的另一个交点为F,
与AC边的另一个交点为F,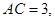
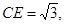 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
![]()
查看答案和解析>>
科目:czsx
来源:2011-2012学年河南安阳九年级5月中考模拟考试数学试卷(解析版)
题型:解答题
如图,在矩形ABCD中,
1.请完成如下操作:①作 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
2.请在(1)的基础上,完成下列问题:
①判断直线BC与圆 的位置关系,并说明理由;
的位置关系,并说明理由;
②若圆 与AC边的另一个交点为F,
与AC边的另一个交点为F,
 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)

查看答案和解析>>
科目:czsx
来源:2012年河南省安阳市中考数学模拟试卷(解析版)
题型:解答题
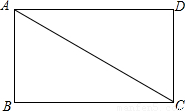
如图,在矩形ABCD中,AD>AB.
(1)请完成如下操作:①作∠BAC的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
(2)请在(1)的基础上,完成下列问题:
①判断直线BC与圆O的位置关系,并说明理由;
②若圆O与AC边的另一个交点为F,AC=3,CE=
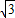
,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:czsx
来源:河南省安阳市2012届九年级5月中考模拟考试数学试题
题型:044
如图,在矩形ABCD中,AD>AB.

(1)请完成如下操作:
①作∠BAC的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
(2)请在(1)的基础上,完成下列问题:
①判断直线BC与圆O的位置关系,并说明理由;
②若圆O与AC边的另一个交点为F,AC=3,CE= ,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在矩形ABCD中,AD>AB.
如图,在矩形ABCD中,AD>AB.
(1)请完成如下操作:①作∠BAC的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
(2)请在(1)的基础上,完成下列问题:
①判断直线BC与圆O的位置关系,并说明理由;
②若圆O与AC边的另一个交点为F,AC=3,CE= ,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和π)
,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:czsx
来源:
题型:
在△ABC中,AD是角平分线,交BC于点D,∠B=60°,∠C=48°,则∠ADB=( )
查看答案和解析>>
科目:czsx
来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版
题型:022
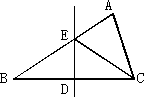
如图,在△ABC中,BC边上的垂直平分线DE交BC边于点D,交AB边于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为________.
查看答案和解析>>
科目:czsx
来源:学习周报 数学 北师大八年级版 2009-2010学年 第19-26期 总第175-182期 北师大版
题型:013
如图,在等腰梯形
ABCD
中,AD
∥BC
,AB
=CD
=a
,DC
边的垂直平分线EF
交BC
边于点E
,且E
为BC
边的中点,DE
∥AB
,则梯形ABCD
的周长等于
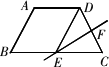
[ ]
查看答案和解析>>
科目:czsx
来源:
题型:单选题
在△ABC中,AD是角平分线,交BC于点D,∠B=60°,∠C=48°,则∠ADB=
- A.
84°
- B.
96°
- C.
72°
- D.
108°
查看答案和解析>>
科目:czsx
来源:2009年北京市延庆县初三数学一模试题
题型:044
如图,正方形ABCD和正方形QMNP,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E.
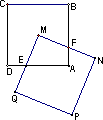
(1)猜想:ME与MF的数量关系
(2)如图,若将原题中的“正方形”改为“菱形”,且∠M=∠B,其它条件不变,探索线段ME与线段MF的数量关系,并加以证明.

(3)如图,若将原题中的“正方形”改为“矩形”,且AB∶BC=1∶2,其它条件不变,探索线段ME与线段MF的数量关系,并说明理由.
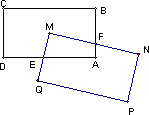
(4)如图,若将原题中的“正方形”改为平行四边形,且∠M=∠B,AB∶BC=m,其它条件不变,求出ME:MF的值.(直接写出答案)
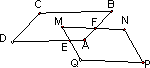
查看答案和解析>>

 24、先阅读下面的材料,然后解答问题:
24、先阅读下面的材料,然后解答问题:


 先阅读下面的材料,然后解答问题:
先阅读下面的材料,然后解答问题: 如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.


 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);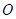 的位置关系,并说明理由;
的位置关系,并说明理由;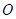 与AC边的另一个交点为F,
与AC边的另一个交点为F,
 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)

 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹); 的位置关系,并说明理由;
的位置关系,并说明理由; 与AC边的另一个交点为F,
与AC边的另一个交点为F,
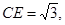 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)


 如图,在矩形ABCD中,AD>AB.
如图,在矩形ABCD中,AD>AB.![]()
![]() 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);![]() 的位置关系,并说明理由;
的位置关系,并说明理由;![]() 与AC边的另一个交点为F,
与AC边的另一个交点为F,![]()
![]() 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
 的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹);
的平分线AE交BC边于点E;②以AC边上一点O为圆心,过A、E两点作圆O(尺规作图,不写作法,保留作图痕迹); 的位置关系,并说明理由;
的位置关系,并说明理由; 与AC边的另一个交点为F,
与AC边的另一个交点为F,
 求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
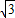 ,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和π)
,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和π)

![]() ,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和Π)
 如图,在矩形ABCD中,AD>AB.
如图,在矩形ABCD中,AD>AB. ,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和π)
,求线段CE、CF与劣弧EF所围成的图形面积.(结果保留根号和π)




