练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >在三角形abc中，角bac=60若ab＝2

    在三角形abc中，角bac=60若ab＝2答案解析

    科目：gzsx 来源： 题型：

    在三角形ABC中，角A，B，C对应的边分别为a，b，c，若∠A=120°，a=2，b=
    2
    		3
    3
    ，则B=（　　）
    A、
    π
    3
    B、
    5π
    6
    C、
    π
    6
    或
    5π
    6
    D、
    π
    6

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在三角形ABC中，角A、B、C所对的边分别是a、b、c，若a=
    		3
    2
    b，A=2B，则cosB等于（　　）
    A、
    		3
    3
    B、
    		3
    4
    C、
    		3
    5
    D、
    		3
    6

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在三角形ABC中，角A，B，C所对的边分别是a，b，c，且acosC，bcosB，ccosA成等差数列，若b=
    		3
    ，则a+c的最大值为（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

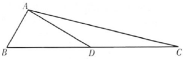
    如图，在三角形ABC中，角A，B，C成等差数列，D是BC边的中点，AD=
    		3
    AB=
    		3
    ．
    （1）求边长AC的长；
    （2）求sin∠DAC的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=(
    		3
    sinωx+cosωx)sin(-
    3π
    2
    +ωx)(0＜ω＜
    1
    2
    )    ，且函数y=f（x）的图象的一个对称中心为(
    5π
    3
    ，a)    ．
    （I）求a和函数f（x）的单调递减区间；
    （II）在三角形ABC中，角A，B，C的对边分别是a，b，c，满足
    2a-c
    b
    =
    cosC
    cosB
    ，求函数f（A）的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在三角形ABC中，角A、B、C满足sinCcosB=（2sinA-sinB）cosC．
    （1）求角C的大小；
    （2）求函数y=2sin2B-cos2A的值域．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•陕西）在三角形ABC中，角A，B，C所对应的长分别为a，b，c，若a=2，B=
    π
    6 
    ，c=2
    		3
    ，则b=
    2
    2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在三角形ABC中，角A、B、C及其对边a，b，c满足：ccosB=（2a-b）cosC．
    （1）求角C的大小；
    （2）求函数y=2sin2B-cos2A的值域．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在三角形ABC中，已知2
    AB
    •
    AC
    =|
    AB
    |•|
    AC
    |    ，设∠CAB=α，
    （1）求角α的值；
    （2）若cos(β-α)=
    4
    		3
    7
    ，其中β∈(
    π
    3
    ，
    5π
    6
    )    ，求cosβ的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在三角形ABC中，角A．B．C成公差大于0的等差数列，
    m
    =(sinAcos
    C-A
    2
    ，cos2A)    ，
    n
    =(2cosA，sin
    C-A
    2
    )
    （1）求
    m
    •
    n
    的取值范围；
    （2）若设A．B．C的对应边分别为a．b．c，求
    a+c
    b
    的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在三角形ABC中，角A、B、C的对边分别为a、b、c，AC边上的高BD=AC，求
    a
    c
    +
    c
    a
    的范围．

    查看答案和解析>>

    科目：gzsx 来源：2015届广东省梅州市高一下第一次质检数学卷（解析版） 题型：解答题

    在三角形ABC中，角A，B，C对应边分别为a，b，c。求证：。

     

    查看答案和解析>>

    科目：gzsx 来源：2013-2014学年江苏苏州高级中学高三12月月考数学试卷（解析版） 题型：解答题

    在三角形ABC中，已知，设∠CAB＝α，

    （1）求角α的值；

    （2）若，其中，求的值.

     

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    在三角形ABC中，角A、B、C的对边分别为a、b、c，AC边上的高BD=AC，求
    a
    c
    +
    c
    a
    的范围．

    查看答案和解析>>

    科目：gzsx 来源：2012-2013学年云南省昆明一中高三（上）第二次双基数学试卷（文科）（解析版） 题型：解答题

    如图，在三角形ABC中，角A，B，C成等差数列，D是BC边的中点，AD=．
    （1）求边长AC的长；
    （2）求sin∠DAC的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：013

    在三角形ABC中，角A、B的对边分别为a、b，A＝2B，则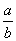的取值范围是（　　 ）

    A．（0，） 　　 　　B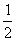．（，1） 　　 　　C．（1，2） 　　 　　D．（0，2）

     

    查看答案和解析>>

    科目：gzsx 来源：2012年陕西省高考数学试卷（文科）（解析版） 题型：解答题

    在三角形ABC中，角A，B，C所对应的长分别为a，b，c，若a=2，B=，c=2，则b=    ．

    查看答案和解析>>

    科目：gzsx 来源：辽宁北票市高级中学2010-2011学年高三第二次月考数学文 题型：解答题

     在三角形ABC中，角所对的边分别为且

    求

    若求的最大值

     

     

     

     

     

     

     

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    在三角形ABC中，角A、B、C的对边分别为a、b、c，AC边上的高BD=AC，求
    a
    c
    +
    c
    a
    的范围．

    查看答案和解析>>

    科目：gzsx 来源：2012-2013学年山东省烟台市莱州一中高三（上）第一次质量检测数学试卷（理科）（解析版） 题型：解答题

    在三角形ABC中，角A、B、C满足sinCcosB=（2sinA-sinB）cosC．
    （1）求角C的大小；
    （2）求函数y=2sin2B-cos2A的值域．

    查看答案和解析>>