练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >如果A是抛物线x2=4y的顶点，过点D（

    如果A是抛物线x2=4y的顶点，过点D（答案解析

    科目：gzsx 来源：云南省模拟题 题型：单选题

    如果A是抛物线x2=4y的顶点，过点D（0，4）的直线l交抛物线x2=4y于B、C两点，那么等于
    [     ]
    A．
    B．0
    C．-3
    D．

    查看答案和解析>>

    科目：gzsx 来源：云南省绿春第一中学2011届高三第二次复习统一检测理科数学试题 题型：013

    如果A是抛物线x2＝4y的顶点，过点D(0，4)的直线l交抛物线x2＝4y于B、C两点，那么·等于

    [　　]
    A．

    B．

    0

    C．

    －3

    D．

    －

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知焦点在x轴上，离心率为
    2
    		5
    5
    的椭圆的一个顶点是抛物线x2=4y的焦点，过椭圆右焦点F的直线l交椭圆于A、B两点，交y轴于点M，且
    MA
    =λ1
    AF
    ，
    MB
    =λ2
    BF
    ．
    （1）求椭圆的方程；
    （2）证明：λ1+λ2为定值．

    查看答案和解析>>

    科目：gzsx 来源：2010年广东省肇庆市高考数学二模试卷（理科）（解析版） 题型：解答题

    已知焦点在x轴上，离心率为的椭圆的一个顶点是抛物线x2=4y的焦点，过椭圆右焦点F的直线l交椭圆于A、B两点，交y轴于点M，且，．
    （1）求椭圆的方程；
    （2）证明：λ1+λ2为定值．

    查看答案和解析>>

    科目：gzsx 来源：2010年广东省肇庆市高考数学二模试卷（文科）（解析版） 题型：解答题

    已知焦点在x轴上，离心率为的椭圆的一个顶点是抛物线x2=4y的焦点，过椭圆右焦点F的直线l交椭圆于A、B两点，交y轴于点M，且，．
    （1）求椭圆的方程；
    （2）证明：λ1+λ2为定值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    注意：第（3）小题平行班学生不必做，特保班学生必须做．
    已知椭圆的焦点在x轴上，它的一个顶点恰好是抛物线x2=4y的焦点，离心率e=
    2
    		5
    ，过椭圆的右焦点F作与坐标轴不垂直的直线l，交椭圆于A、B两点．
    （1）求椭圆的标准方程；
    （2）设点M（m，0）是线段OF上的一个动点，且(
    MA
    +
    MB
    )⊥
    AB
    ，求m的取值范围；
    （3）设点C是点A关于x轴的对称点，在x轴上是否存在一个定点N，使得C、B、N三点共线？若存在，求出定点N的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2011•重庆模拟）已知焦点在x轴上的椭圆的左右焦点分别为F1、F2，椭圆的一个顶点恰好是抛物线x2=4y的焦点，点P是椭圆上一动点且△F1F2P的面积最大值为2．
    （Ⅰ）求椭圆方程；
    （Ⅱ）过椭圆的右焦点F2作与坐标轴不垂直的直线交椭圆于A，B两点，点M（m，0）是x轴上不同于原点的一个动点，求满足条件(
    MA
    +
    MB
    )⊥
    AB
    的实数m的取值范围．

    查看答案和解析>>

    科目：gzsx 来源：2012-2013学年福建省三明一中高三（上）第三次月考数学试卷（理科）（解析版） 题型：解答题

    注意：第（3）小题平行班学生不必做，特保班学生必须做．
    已知椭圆的焦点在x轴上，它的一个顶点恰好是抛物线x2=4y的焦点，离心率，过椭圆的右焦点F作与坐标轴不垂直的直线l，交椭圆于A、B两点．
    （1）求椭圆的标准方程；
    （2）设点M（m，0）是线段OF上的一个动点，且，求m的取值范围；
    （3）设点C是点A关于x轴的对称点，在x轴上是否存在一个定点N，使得C、B、N三点共线？若存在，求出定点N的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

        已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线x2=4y的焦点，离心率等于．

    ( I )求椭圆C的方程；

    (II)过椭圆C的右焦点F作直线l交椭圆C于A，B两点，交y轴于M点，若，求证为定值．

    查看答案和解析>>

    科目：gzsx 来源：2010-2011学年重庆市主城八区高三第二次调研数学试卷（理科）（解析版） 题型：解答题

    已知焦点在x轴上的椭圆的左右焦点分别为F1、F2，椭圆的一个顶点恰好是抛物线x2=4y的焦点，点P是椭圆上一动点且△F1F2P的面积最大值为2．
    （Ⅰ）求椭圆方程；
    （Ⅱ）过椭圆的右焦点F2作与坐标轴不垂直的直线交椭圆于A，B两点，点M（m，0）是x轴上不同于原点的一个动点，求满足条件的实数m的取值范围．

    查看答案和解析>>

    科目：gzsx 来源：2011年重庆市九区高三4月调研数学试卷（理科）（解析版） 题型：解答题

    已知焦点在x轴上的椭圆的左右焦点分别为F1、F2，椭圆的一个顶点恰好是抛物线x2=4y的焦点，点P是椭圆上一动点且△F1F2P的面积最大值为2．
    （Ⅰ）求椭圆方程；
    （Ⅱ）过椭圆的右焦点F2作与坐标轴不垂直的直线交椭圆于A，B两点，点M（m，0）是x轴上不同于原点的一个动点，求满足条件的实数m的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知A，B是抛物线x2=4y上两个动点，且直线AO与直线BO的倾斜角之和为
    π4
    ，试证明直线AB过定点．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

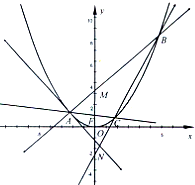    如图，A是抛物线x2=4y上异于原点的任意一点，F为抛物线的焦点，l为抛物线在A点处的切线，点B、C在抛物线上，AB⊥l且交y轴于M，点A、F、C三点共线，直线BC交y轴于N．
    （1）求证：|AF|=|MF|；
    （2）求|MN|的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    13、已知抛物线x2=4y的焦点F和点A（-1，8），P为抛物线上一点，则|PA|+|PF|的最小值是
    9
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知抛物线x2=4y的焦点F和点A（-1，8），P为抛物线上一点，则|PA|+|PF|的最小值是（　　）
    A、16B、12C、9D、6

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•金华模拟）如图，A是抛物线x2=4y上异于原点的任意一点，F为抛物线的焦点，l为抛物线在A点处的切线，点B、C在抛物线上，AB⊥l且交y轴于M，点A、F、C三点共线，直线BC交y轴于N．
    （1）求证：|AF|=|MF|；
    （2）求|MN|的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知抛物线x2=4y的焦点F和点A（-1，4），P为抛物线上一点，则|PA|+|PF|的最小值是
    5
    5
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C：
    y2
    a2
    +
    x2
    b2
    =1（a＞b＞0）的两焦点与短轴的一个端点连结成等腰直角三角形，直线l：x-y-b=0是抛物线x2=4y的一条切线．
    （1）求椭圆方程；
    （2）直线l交椭圆C于A、B两点，若点P满足
    OP
    +
    OA
    +
    OB
    =
    0
    （O为坐标原点），判断点P是否在椭圆C上，并说明理由．

    查看答案和解析>>

    科目：gzsx 来源：2010-2011学年云南省高三第二次统一检测数学试卷 题型：选择题

    如果A是抛物线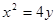的顶点，过点D（0，4）的直线交抛物线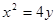于B、C两点，那么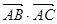等于（    ）

        A．             B．0              C．-3             D．

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：解答题

    已知A，B是抛物线x2=4y上两个动点，且直线AO与直线BO的倾斜角之和为数学公式，试证明直线AB过定点．

    查看答案和解析>>