九年级数学配套 当x为何值时 窗户的透光面积最大 那个题答案解析
科目:czsx
来源:
题型:
把一根长120cm的铁丝弯曲成一个长方形.
(1)设它的长为xcm,面积为ycm2,写出y(cm2)与x(cm)的函数关系式;
(2)当x为何值时,这个长方形面积最大,是多少?
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
把一根长120cm的铁丝弯曲成一个长方形.
(1)设它的长为xcm,面积为ycm2,写出y(cm2)与x(cm)的函数关系式;
(2)当x为何值时,这个长方形面积最大,是多少?
查看答案和解析>>
科目:czsx
来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标
题型:044
已知一三角形纸片ABC,面积为25,BC边长为10,∠B和∠C都是锐角,M为AB边上一动点,M与点A,B不重合,过点M作MN∥BC交AC于点N,设MN=x.如图所示.

(1)用x表示△AMN的面积S△AMN;
(2)将△AMN沿MN折叠,使△AMN紧贴四边形BCMN(边AM,AN落在四边形BCNM所在的平面内),设点A落在平面BCNM内的点为 ,△
,△ MN与四边形BCNM重叠部分的面积为y.
MN与四边形BCNM重叠部分的面积为y.
①试求y关于x的函数关系式,并写出自变量x的取值范围;
②当x为何值时,重叠部分面积最大,最大为多少?
查看答案和解析>>
科目:czsx
来源:
题型:解答题
把一根长120cm的铁丝弯曲成一个长方形.
(1)设它的长为xcm,面积为ycm2,写出y(cm2)与x(cm)的函数关系式;
(2)当x为何值时,这个长方形面积最大,是多少?
查看答案和解析>>
科目:czsx
来源:
题型:
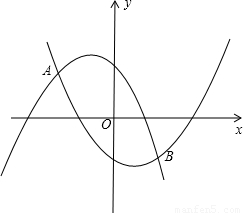
如图,抛物线y
1=-ax
2-ax+1经过点P(-
,
),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D
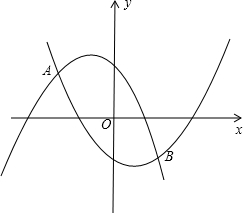
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
查看答案和解析>>
科目:czsx
来源:
题型:
某房地产开发公司计划兴建A,B两种房型的住房80套,该公司所筹资金不少于2090万元,但不超过2096万元.且所筹资金全部用于建房,两种房型的建房成本和售价如下表:
| |
A种房型 |
B种房型 |
| 成本(万元/套) |
25 |
28 |
| 售价(万元/套) |
30 |
34 |
(1)该公司对这两种房型住房有哪几种建房方案?
(2)设该公司建A型房x套,公司获得的总利润(总利润=总销售额-总成本)为W万元,求W与x之间的函数关系.
(3)当x为何值时,所获利润最大?最大利润是多少?
查看答案和解析>>
科目:czsx
来源:
题型:
如图,直角梯形OABC中,∠COA=90°,BC∥OA,OA=6,BC=3,AB=
3,已知抛物线经过O、A、B
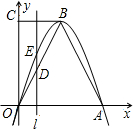
三点.
(1)求抛物线的解析式;
(2)平行与y轴的直线l从点O向终点A匀速运动,速度是每秒1个单位长,运动时间为t秒.直线l交折线段OBA于点D,交抛物线于点E.问:当t为何值时,线段DE有最大值?最大值是多少?
(3)探索:坐标平面内是否存在一点F,使得以C、B、D、F为顶点的四边形是菱形?如果存在,请直接写出点F的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
在同一坐标系中,画出函数y=-x2和y=-x2+1的图象,根据图象回答:
(1)抛物线y=-x2+1经过怎样的平移得到抛物线y=-x2
(2)对于函数y=-x2+1:
①当x为何值时,y随x的增大而减小?
②当x为何值时,函数y有最大值?最大值是多少?
③求y=-x2+1的图象与x轴、y轴的交点坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
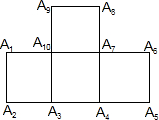
附加题:(1)如图,在四个正方形拼接成的图形中,以A
1、A
2、A
3、…、A
10这十个点中任意三点为顶点,共能组成
个等腰直角三角形.
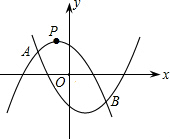
(2)已知y
1=-ax
2-ax+1的顶点P的纵坐标为
,且与抛物线y
2=ax
2-ax-1相交于A,B两点.设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
查看答案和解析>>
科目:czsx
来源:第6章《二次函数》常考题集(23):6.4 二次函数的应用(解析版)
题型:解答题
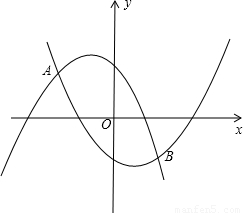
如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》常考题集(24):2.8 二次函数的应用(解析版)
题型:解答题
如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
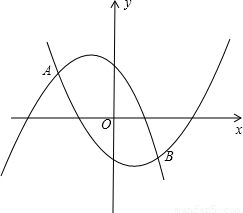
如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,直角梯形OABC中,∠COA=90°,BC∥OA,OA=6,BC=3,AB=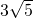 ,已知抛物线经过O、A、B
,已知抛物线经过O、A、B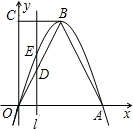 三点.
三点.
(1)求抛物线的解析式;
(2)平行与y轴的直线l从点O向终点A匀速运动,速度是每秒1个单位长,运动时间为t秒.直线l交折线段OBA于点D,交抛物线于点E.问:当t为何值时,线段DE有最大值?最大值是多少?
(3)探索:坐标平面内是否存在一点F,使得以C、B、D、F为顶点的四边形是菱形?如果存在,请直接写出点F的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第6章《二次函数》中考题集(38):6.4 二次函数的应用(解析版)
题型:解答题
如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?

查看答案和解析>>
科目:czsx
来源:2009年福建省泉州市实验中学中考数学模拟试卷(解析版)
题型:解答题
(2008•南昌)如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?

查看答案和解析>>
科目:czsx
来源:2011年江苏省泰州市姜堰市南苑学校九年级(下)期中数学试卷(解析版)
题型:解答题
如图,直角梯形OABC中,∠COA=90°,BC∥OA,OA=6,BC=3,AB=

,已知抛物线经过O、A、B三点.
(1)求抛物线的解析式;
(2)平行与y轴的直线l从点O向终点A匀速运动,速度是每秒1个单位长,运动时间为t秒.直线l交折线段OBA于点D,交抛物线于点E.问:当t为何值时,线段DE有最大值?最大值是多少?
(3)探索:坐标平面内是否存在一点F,使得以C、B、D、F为顶点的四边形是菱形?如果存在,请直接写出点F的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(35):23.5 二次函数的应用(解析版)
题型:解答题
如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?

查看答案和解析>>
科目:czsx
来源:2008年全国中考数学试题汇编《二次函数》(07)(解析版)
题型:解答题
(2008•南昌)如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?

查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(38):34.4 二次函数的应用(解析版)
题型:解答题
如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
查看答案和解析>>
科目:czsx
来源:2009年数学中考模拟试卷(15)(解析版)
题型:解答题
(2008•南昌)如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?

查看答案和解析>>


![]() ,△
,△![]() MN与四边形BCNM重叠部分的面积为y.
MN与四边形BCNM重叠部分的面积为y. 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?  三点.
三点.

 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.
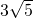 ,已知抛物线经过O、A、B
,已知抛物线经过O、A、B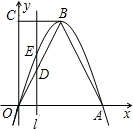 三点.
三点. ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.
 ,已知抛物线经过O、A、B三点.
,已知抛物线经过O、A、B三点.
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.