练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >二次函数y=ax2+ax+2（a＞0）在

    二次函数y=ax2+ax+2（a＞0）在答案解析

    科目：gzsx 来源： 题型：

    二次函数y=ax2+ax+2（a＞0）在R上的最小值为f（a）
    （1）写出函数f（a）的解析式；
    （2）用定义证明函数f（a）的奇偶性；
    （3）判断f（a）在[1，5]上的单调性，并加以证明．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    分类讨论，二次函数y=ax2+bx+c（a＞0）在区间[m，n]上的最值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：解答题

    分类讨论，二次函数y=ax2+bx+c（a＞0）在区间[m，n]上的最值．

    查看答案和解析>>

    科目：gzsx 来源：2010年高考数学专项复习：二次函数（解析版） 题型：解答题

    分类讨论，二次函数y=ax2+bx+c（a＞0）在区间[m，n]上的最值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    二次函数y=ax2+bx+c（a＜0）与x轴的两个交点为(-
    		2
    ，0)，(
    		2
    ，0)    ，则ax2+bx+c＜0的解为（　　）
    A、-
    		2
    ＜x＜
    		2
    B、x＞
    		2
    或x＜-
    		2
    C、x≠±
    		2
    D、Φ

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    二次函数y=ax2+bx+c（a＞0），满足f（5）=f（-1），那么（　　）

    查看答案和解析>>

    科目：gzsx 来源：2009-2010学年浙江省宁波市北仑中学高一（上）期中数学试卷（解析版） 题型：选择题

    二次函数y=ax2+bx+c（a＜0）与x轴的两个交点为，则ax2+bx+c＜0的解为（ ）
    A．
    B．
    C．
    D．Φ

    查看答案和解析>>

    科目：gzsx 来源： 题型：单选题

    二次函数y=ax2+bx+c（a＜0）与x轴的两个交点为数学公式，则ax2+bx+c＜0的解为


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      数学公式
    4. D.
      Φ

    查看答案和解析>>

    科目：gzsx 来源： 题型：

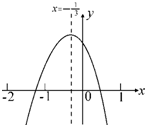
    精英家教网小轩从如图所示的二次函数y=ax2+bx+c（a≠0）的图象中，观察得出了下面五条信息：①ab＞0；②a+b+c＜0；③b+2c＞0；④a-2b+4c＞0；⑤a=
    3
    2
    b    ，你认为其中正确信息的个数有（　　）
    A、2个B、3个C、4个D、5个

    查看答案和解析>>

    科目：gzsx 来源： 题型：

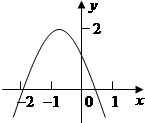
    如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1，x2．其中-2＜x1＜-1，0＜x2＜1，
    下列结论：
    ①4a-2b+c＜0；  
    ②2a-b＜0； 
    ③a＜-1； 
    ④b2+8a＞4ac．
    其中正确的有（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1、x2，其中-2＜x1＜-1，0＜x2＜1．下列结论：①4a-2b+c＜0；②2a-b＜0；③a＜-1；④b2+8a＞4ac．其中正确结论的序号是
    ①②③④
    ①②③④
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

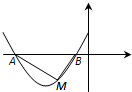
    二次函数y=ax2+bx+c（a≠0）的图象如图所示，M（n，-2）是图象上的一点，A、B是二次函数图象与x轴的两个交点，且AM⊥BM，则a的值为（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

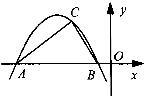
    如图，已知二次函数y=ax2+bx+c（a，b，c为实数，a≠0）的图象过点C（t，2），且与x轴交于A，B两点，若AC⊥BC，则a的值为
    -
    1
    2
    -
    1
    2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若二次函数y=ax2+4x-2有零点，则实数a的取值范围是
    a≥-2
    a≥-2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    二次函数y=ax2+bx+c（a≠0）是偶函数，则实数b等于（　　）
    A、1B、0C、-1D、2

    查看答案和解析>>

    科目：gzsx 来源：2011年辽宁省丹东市高考数学模拟试卷（理科）（解析版） 题型：选择题

    二次函数y=ax2+bx+c（a≠0）是偶函数，则实数b等于（ ）
    A．1
    B．0
    C．-1
    D．2

    查看答案和解析>>

    科目：gzsx 来源：2011-2012学年甘肃甘谷一中宏志班选拔考试数学试卷（解析版） 题型：选择题

    如图为二次函数y=ax2+bx+c（a≠0）的图象，则下列说法：

    ①a＞0   ②2a+b=0  ③a+b+c＞0  ④当﹣1＜x＜3时，y＞0

    其中正确的个数为（　　）

    A．1              B．2           C．3            D．4

     

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：单选题

    二次函数y=ax2+bx+c（a≠0）是偶函数，则实数b等于（　　）
    A．1B．0C．-1D．2

    查看答案和解析>>

    科目：gzsx 来源： 题型：

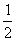
    若不等式ax2+bx+2＞0的解集为{x|-＜x＜},二次函数y=ax2+bx+2在［-,］上的值域为［m,n］，则m+n=__________.

    查看答案和解析>>

    科目：gzsx 来源：2012-2013学年重庆94中高三（上）第五次月考数学试卷（解析版） 题型：选择题

    如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1，x2．其中-2＜x1＜-1，0＜x2＜1，
    下列结论：
    ①4a-2b+c＜0；  
    ②2a-b＜0； 
    ③a＜-1； 
    ④b2+8a＞4ac．
    其中正确的有（ ）

    A．1个
    B．2个
    C．3个
    D．4个

    查看答案和解析>>