
科目:czsx 来源: 题型:
 已知正方形ABCD的边长是2,E是CD的中点,动点P从点A出发,沿A→B→C→E运动,到达E点即停止运动,若点P经过的路程为x,△APE的面积记为y,试求出y与x之间的函数解析式,并求出当y=
已知正方形ABCD的边长是2,E是CD的中点,动点P从点A出发,沿A→B→C→E运动,到达E点即停止运动,若点P经过的路程为x,△APE的面积记为y,试求出y与x之间的函数解析式,并求出当y=| 1 | 3 |
科目:czsx 来源: 题型:
已知正方形ABCD的边长是2,E是CD的中点,动点P从点A出发,沿A→B→C→E运动,到达E点即停止运动,若点P经过的路程为x,△APE的面积记为y,试求出y与x之间的函数解析式,并求出当y=![]() 时,x的值.
时,x的值.

科目:czsx 来源:2012届湖北省鄂州市八年级上学期期末考试数学试卷 题型:解答题
已知正方形ABCD的边长是2,E是CD的中点,动点P从点A出发,沿A→B→C→E运动,到达E点即停止运动,若点P经过的路程为x,△APE的面积记为y,试求出y与x之间的函数解析式,并求出当y= 时,x的值.
时,x的值.

科目:czsx 来源:2010—2011学年湖北省鄂州市八年级上学期期末考试数学试卷 题型:解答题
已知正方形ABCD的边长是2,E是CD的中点,动点P从点A出发,沿A→B→C→E运动,到达E点即停止运动,若点P经过的路程为x,△APE的面积记为y,试求出y与x之间的函数解析式,并求出当y=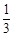 时,x的值.
时,x的值.
科目:czsx 来源: 题型:
 时,x的值.
时,x的值.
科目:czsx 来源:湖北省期末题 题型:解答题
 时,x的值.
时,x的值.
科目:czsx 来源: 题型:解答题
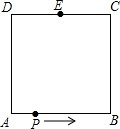 已知正方形ABCD的边长是2,E是CD的中点,动点P从点A出发,沿A→B→C→E运动,到达E点即停止运动,若点P经过的路程为x,△APE的面积记为y,试求出y与x之间的函数解析式,并求出当y=
已知正方形ABCD的边长是2,E是CD的中点,动点P从点A出发,沿A→B→C→E运动,到达E点即停止运动,若点P经过的路程为x,△APE的面积记为y,试求出y与x之间的函数解析式,并求出当y= 时,x的值.
时,x的值.科目:czsx 来源:2012届湖北省鄂州市八年级上学期期末考试数学试卷 题型:解答题
我市劲威乡A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元.
1.请填写下表

2.求出yA、yB与x之间的函数解析式;
3.试讨论A、B两村中,哪个村的运费最少;
4.考虑B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
科目:czsx 来源:2010—2011学年湖北省鄂州市八年级上学期期末考试数学试卷 题型:解答题
我市劲威乡A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元.
【小题1】请填写下表
【小题2】求出yA、yB与x之间的函数解析式;
【小题3】试讨论A、B两村中,哪个村的运费最少;
【小题4】考虑B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
我市劲威乡A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元.
1.请填写下表
2.求出yA、yB与x之间的函数解析式;
3.试讨论A、B两村中,哪个村的运费最少;
4.考虑B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
科目:czsx 来源: 题型:
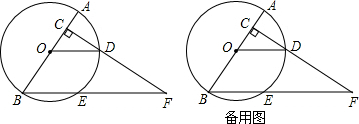
 |
| ED |
 |
| BE |
科目:czsx 来源: 题型:
 .
.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 2 |
科目:czsx 来源: 题型: