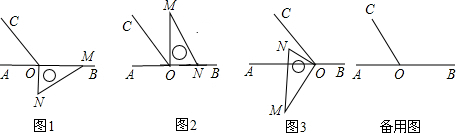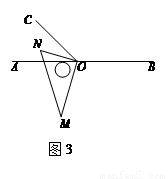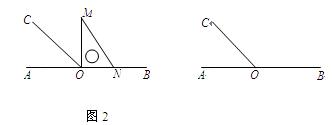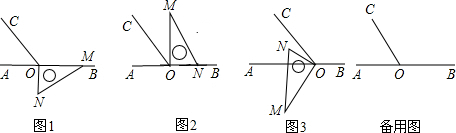精英家教网 >
试题搜索列表 >把三角形ABC绕点A旋转至三角形ADE的位置,使点D落在BC边上若角1+角2=110度,则角ABC的度数是
把三角形ABC绕点A旋转至三角形ADE的位置,使点D落在BC边上若角1+角2=110度,则角ABC的度数是答案解析
科目:czsx
来源:
题型:
如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为
90
90
度;
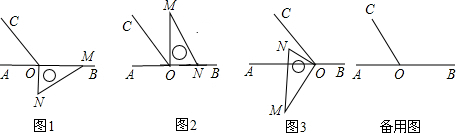
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.

(1)将图1中的三角板绕点O按顺时针方向旋转至图2的位置,使得OM落在射线OA上,此时ON旋转的角度为
90
90
°;
(2)继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得OM在∠BOC的内部,则∠BON-∠COM=
30
30
°;
(3)在上述直角三角板从图1旋转到图3的位置的过程中,若三角板绕点O按每秒钟15°的速度旋转,当OM恰为∠BOC的平分线时,此时,三角板绕点O的运动时间为
16
16
秒,简要说明理由.
查看答案和解析>>
科目:czsx
来源:2015届湖北省黄冈市七年级上学期期末考试数学试卷(解析版)
题型:解答题
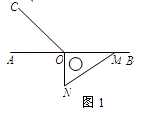
如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:3,将一直角△MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.绕点O顺时针旋转△MON,其中旋转的角度为α(0<α<360°).

(1)将图1中的直角△MON旋转至图2的位置,使得ON落在射线OB上,此时α为 度;

(2)将图1中的直角△MON旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM
与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角△MON从图1旋转到图3的位置的过程中,若直角△MON绕点O按每秒25°的速度顺时针旋转,当直角△MON的直角边ON所在直线恰好平分∠AOC时,求此时直角△MON绕点O的运动时间t的值.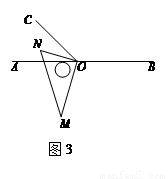
查看答案和解析>>
科目:czsx
来源:2012-2013学年湖北省黄冈市启黄中学七年级上学期期末考试数学试卷(带解析)
题型:解答题
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为______度;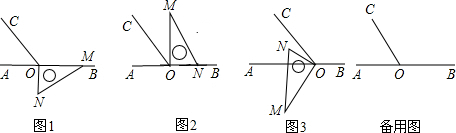
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
查看答案和解析>>
科目:czsx
来源:
题型:

22、如图,△ABC按逆时针旋转至△AB′C′的位置,使AC平分BB′.
求证:AB′平分CC′.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
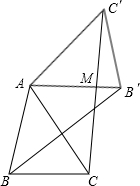 如图,△ABC按逆时针旋转至△AB′C′的位置,使AC平分BB′.
如图,△ABC按逆时针旋转至△AB′C′的位置,使AC平分BB′.
求证:AB′平分CC′.
查看答案和解析>>
科目:czsx
来源:《第1章 证明(二)》2009年水平测试C卷(解析版)
题型:解答题
如图,△ABC按逆时针旋转至△AB′C′的位置,使AC平分BB′.
求证:AB′平分CC′.

查看答案和解析>>
科目:czsx
来源:《第1章 证明(二)》2011年单元测试卷(三)(解析版)
题型:解答题
如图,△ABC按逆时针旋转至△AB′C′的位置,使AC平分BB′.
求证:AB′平分CC′.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,△ABC按逆时针旋转至△AB′C′的位置,使AC平分BB′.
求证:AB′平分CC′.
查看答案和解析>>
科目:czsx
来源:
题型:
两张透明的三角形胶片完全重合摆放,如图1,所示△ABC和△DEF,将△DEF沿着公共边翻折180°,得到如图2,再把△DEF绕点B(E)按顺时针方向旋转,对应边AC与DF所在直线交于O
(1)当△DEF旋转至图3的位置即点B(E),F,A在同一条直线上,判断∠AFD与∠DCA是否相等,并予以证明;
(2)当△DEF旋转至B(E),F,A不共线时,画出其中一种图形,再判断(1)中结论是否还成立?并说明理由.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
两张透明的三角形胶片完全重合摆放,如图1,所示△ABC和△DEF,将△DEF沿着公共边翻折180°,得到如图2,再把△DEF绕点B(E)按顺时针方向旋转,对应边AC与DF所在直线交于O
(1)当△DEF旋转至图3的位置即点B(E),F,A在同一条直线上,判断∠AFD与∠DCA是否相等,并予以证明;
(2)当△DEF旋转至B(E),F,A不共线时,画出其中一种图形,再判断(1)中结论是否还成立?并说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
两张透明的三角形胶片完全重合摆放,如图1,所示△ABC和△DEF,将△DEF沿着公共边翻折180°,得到如图2,再把△DEF绕点B(E)按顺时针方向旋转,对应边AC与DF所在直线交于O
(1)当△DEF旋转至图3的位置即点B(E),F,A在同一条直线上,判断∠AFD与∠DCA是否相等,并予以证明;
(2)当△DEF旋转至B(E),F,A不共线时,画出其中一种图形,再判断(1)中结论是否还成立?并说明理由.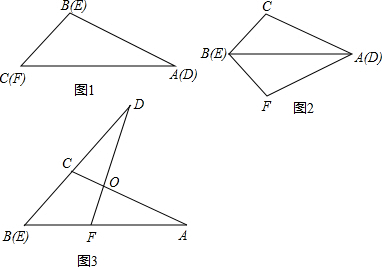
查看答案和解析>>
科目:czsx
来源:
题型:
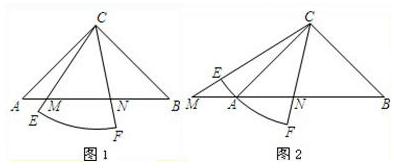
25、已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN
2=AM
2+BN
2;
(思路点拨:考虑MN
2=AM
2+BN
2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN
2=AM
2+BN
2是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
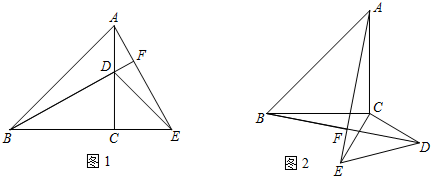
如图1,已知△ABC与△DCE都是等腰直角三角形,AC=BC,DC=EC,∠ACB=∠DCE=90°,点D在AC上,直线BD交AE于点F.
(1)请补充完整证明“BD=AE,BF⊥AE”的推理过程;
证明:在△ACE与△BCD中
∵(
AC=BC,∠DCB=∠ECA,DC=EC
AC=BC,∠DCB=∠ECA,DC=EC
)
∴△ACE≌△BCD(SAS)
∴BD=AE,∠CAE=∠CBD(全等三角形的对应角相等)
∵∠ACE=90°
∴∠CAE+∠AEC=90°(
直角三角形的两锐角互余
直角三角形的两锐角互余
)
∴∠CBD+∠AEC=90°(等量代换)
∴
∠BFE=90°
∠BFE=90°
∴BF⊥AE(垂直的定义)
(2)将△DCE绕着点C旋转,在旋转过程中保持△DCE的大小与形状均不变,那么,当△DCE旋转至图2的位置时,(1)中的结论是否仍然成立?为什么?
查看答案和解析>>
科目:czsx
来源:第22章《圆(上)》常考题集(07):22.3 圆的对称性(解析版)
题型:解答题
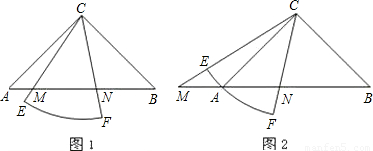
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN
2=AM
2+BN
2;
(思路点拨:考虑MN
2=AM
2+BN
2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN
2=AM
2+BN
2是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:czsx
来源:2009年安徽省巢湖市初中毕业班联考数学试卷(解析版)
题型:解答题
(2008•天津)已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN
2=AM
2+BN
2;
(思路点拨:考虑MN
2=AM
2+BN
2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN
2=AM
2+BN
2是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:czsx
来源:第3章《圆》常考题集(10):3.1 圆(解析版)
题型:解答题
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN
2=AM
2+BN
2;
(思路点拨:考虑MN
2=AM
2+BN
2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN
2=AM
2+BN
2是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:czsx
来源:第28章《圆》常考题集(10):28.1 圆的认识(解析版)
题型:解答题
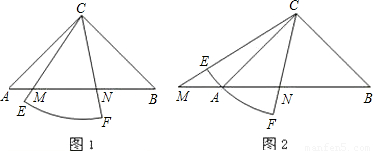
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN
2=AM
2+BN
2;
(思路点拨:考虑MN
2=AM
2+BN
2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN
2=AM
2+BN
2是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:czsx
来源:第3章《圆》常考题集(06):3.2 圆的对称性(解析版)
题型:解答题
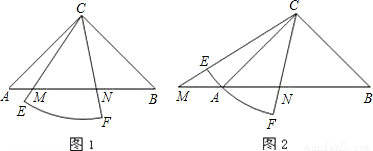
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN
2=AM
2+BN
2;
(思路点拨:考虑MN
2=AM
2+BN
2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN
2=AM
2+BN
2是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>