
科目:gzsx 来源:2014届湖北省教学合作高三10月联考文科数学试卷(解析版) 题型:解答题
已知函数
 d的最大值为2,
d的最大值为2, 是集合
是集合 中的任意两个元素,且
中的任意两个元素,且 的最小值为
的最小值为 .
.
(1)求函数 的解析式及其对称轴;
的解析式及其对称轴;
(2)若 ,求
,求 的值.
的值.
科目:gzsx 来源: 题型:

图1-2-8
科目:gzsx 来源:高中数学全解题库(国标苏教版·必修4、必修5) 苏教版 题型:044
在数列{an}中,已知![]() (n∈N*).
(n∈N*).
(1)写出al0,an+1,![]() ;
;
(2)![]() 是否是数列中的项?若是,是第几项?
是否是数列中的项?若是,是第几项?
科目:gzsx 来源:四川省南充高中2010届高三5月适应性考试(理) 题型:解答题
已知函数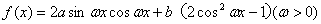 在
在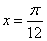 时取最大值2。
时取最大值2。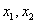 是集合
是集合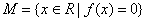 中的任意两个元素,|
中的任意两个元素,|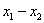 |的最小值为
|的最小值为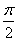 。
。
(I)求a、b的值;
(II)若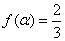 ,求
,求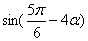 的值。
的值。
科目:gzsx 来源:山东省潍坊市2010年高考模拟训练A(理) 题型:解答题
已知函数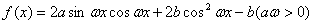 在
在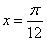 时取最大值2。
时取最大值2。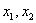 是集合
是集合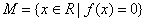 中的任意两个元素,|
中的任意两个元素,|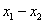 |的最小值为
|的最小值为 。
。
(I)求a、b的值;
(II)若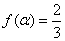 ,求
,求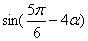 的值。
的值。
科目:gzsx 来源:2011-2012学年上海市徐汇区高三4月学习能力诊断理科数学试卷(解析版) 题型:解答题
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数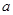 使得数列
使得数列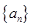 满足:若
满足:若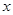 是数列
是数列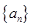 中的一项,则
中的一项,则 也是数列
也是数列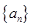 中的一项,称数列
中的一项,称数列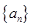 为“兑换数列”,常数
为“兑换数列”,常数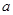 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: 是“兑换系数”为
是“兑换系数”为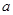 的“兑换数列”,求
的“兑换数列”,求 和
和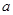 的值;
的值;
(2)已知有穷等差数列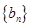 的项数是
的项数是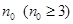 ,所有项之和是
,所有项之和是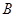 ,求证:数列
,求证:数列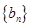 是“兑换数列”,并用
是“兑换数列”,并用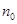 和
和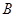 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列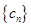 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
科目:gzsx 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分.
已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(1) 若![]() ,是否存在
,是否存在![]() ,有
,有![]() 说明理由;
说明理由;
(2) 找出所有数列![]() 和
和![]() ,使对一切
,使对一切![]() ,
,![]() ,并说明理由;
,并说明理由;
(3) 若![]() 试确定所有的
试确定所有的![]() ,使数列
,使数列![]() 中存在某个连续
中存在某个连续![]() 项的和是数列
项的和是数列![]() 中的一项,请证明.
中的一项,请证明.
科目:gzsx 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列。
的等比数列。
(1) 若![]() ,是否存在
,是否存在![]() ,有
,有![]() 说明理由;
说明理由; ![]()
![]()
(2) 找出所有数列![]() 和
和![]() ,使对一切
,使对一切![]() ,
,![]() ,并说明理由;
,并说明理由;
(3) 若![]() 试确定所有的
试确定所有的![]() ,使数列
,使数列![]() 中存在某个连续
中存在某个连续![]() 项的和是数列
项的和是数列![]() 中的一项,请证明。
中的一项,请证明。
科目:gzsx 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列。
的等比数列。
若![]() ,是否存在
,是否存在![]() ,有
,有![]() 说明理由;
说明理由;
找出所有数列![]() 和
和![]() ,使对一切
,使对一切![]() ,
,![]() ,并说明理由;
,并说明理由;
若![]() 试确定所有的
试确定所有的![]() ,使数列
,使数列![]() 中存在某个连续
中存在某个连续![]() 项的和是数列
项的和是数列![]() 中的一项,请证明。
中的一项,请证明。
科目:gzsx 来源: 题型:
(2009年上海卷理)(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列。
的等比数列。
若![]() ,是否存在
,是否存在![]() ,有
,有![]() 说明理由;
说明理由;
找出所有数列![]() 和
和![]() ,使对一切
,使对一切![]() ,
,![]() ,并说明理由;
,并说明理由;
若![]() 试确定所有的
试确定所有的![]() ,使数列
,使数列![]() 中存在某个连续
中存在某个连续![]() 项的和是数列
项的和是数列![]() 中的一项,请证明。
中的一项,请证明。
科目:gzsx 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列。
的等比数列。
若![]() ,是否存在
,是否存在![]() ,有
,有![]() 说明理由;
说明理由;
找出所有数列![]() 和
和![]() ,使对一切
,使对一切![]() ,
,![]() ,并说明理由;
,并说明理由;
若![]() 试确定所有的
试确定所有的![]() ,使数列
,使数列![]() 中存在某个连续
中存在某个连续![]() 项的和是数列
项的和是数列![]() 中的一项,请证明。
中的一项,请证明。
科目:gzsx 来源:2009年普通高等学校招生全国统一考试理科数学(上海卷) 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分.
已知 是公差为
是公差为 的等差数列,
的等差数列, 是公比为
是公比为 的等比数列.
的等比数列.
(1) 若 ,是否存在
,是否存在 ,有
,有 说明理由;
说明理由;
(2) 找出所有数列 和
和 ,使对一切
,使对一切 ,
, ,并说明理由;
,并说明理由;
(3) 若 试确定所有的
试确定所有的 ,使数列
,使数列 中存在某个连续
中存在某个连续 项的和是数列
项的和是数列 中的一项,请证明.
中的一项,请证明.
科目:gzsx 来源: 题型:
| m |
| 1 |
| 2 |
| n |
| m |
| n |
科目:gzsx 来源: 题型:
| 1 |
| 2 |
| ||
| 2 |
|
科目:gzsx 来源: 题型: