
科目:gzsx 来源:广州省2009-2010学年高二学科竞赛(数学理) 题型:解答题
(本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表,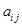 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为 ,若已知
,若已知
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
(1)求 的值;
的值;
(2)求用 表示
表示 的代数式;
的代数式;
(3)设表中对角线上的数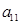 ,
,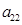 ,
, ,……,
,……,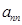 组成一列数列,设Tn=
组成一列数列,设Tn=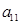 +
+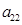 +
+ +……+
+……+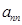 求使不等式
求使不等式 成立的最小正整数n.
成立的最小正整数n.
科目:gzsx 来源: 题型:
已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<logmab<1,则m的取值范围是( )
A.m>1 B.1<m<8 C.m>8 D.0<m<1或m>8
科目:gzsx 来源: 题型:
A.m>1 B.1<m<8 C.m>8 D.0<m<1或m>8
科目:gzsx 来源:广州省高州一中2009-2010学年高二学科竞赛(数学理) 题型:解答题
(本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表, 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为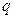 ,若已知
,若已知
 | 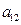 |  | … | 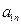 |
 |  | 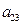 | … |  |
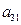 |  | 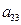 | … |  |
| … | … | … | … | … |
 |  |  | … |  |
 的值;
的值;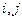 表示
表示 的代数式;
的代数式; ,
, ,
,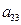 ,……,
,……, 组成一列数列,设Tn=
组成一列数列,设Tn= +
+ +
+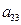 +……+
+……+ 求使不等式
求使不等式 成立的最小正整数n.
成立的最小正整数n. 科目:gzsx 来源: 题型:
A.等差数列,但不成等比数列
B.等比数列而非等差数列
C.等比数列,也可能成等差数列
D.既不是等比数列,又不是等差数列
科目:gzsx 来源: 题型:
A.是等比数列而非等差数列 B.是等差数列而非等比数列
C.既是等比数列又是等差数列 D.既不是等比数列又不是等差数列
科目:gzsx 来源:2014届山东省聊城市高二第四次模块检测理科数学卷(解析版) 题型:选择题
已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<log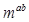 <1,则m的取值范围是( )
<1,则m的取值范围是( )
A.m>1 B.1<m<8
C.m>8 D.0<m<1或m>8
科目:gzsx 来源: 题型:
A.等差数列,但不成等比数列 B.等比数列而非等差数列
C.等比数列,也可能成等差数列 D.既不是等比数列,又不是等差数列
科目:gzsx 来源: 题型:
| an | an+t |
科目:gzsx 来源: 题型:
| 1 |
| ak |
| 1 |
| ap |
| 1 |
| ar |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源:2012届北京市高三第一学期期中考试理科数学试卷 题型:解答题
设等差数列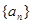 的公差
的公差 且
且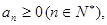 记
记 为数列
为数列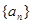 的前
的前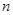 项和.
项和.
(1)若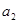 、
、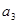 、
、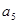 成等比数列,且
成等比数列,且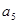 、
、 的等差中项为
的等差中项为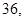 求数列
求数列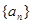 的通项公式;
的通项公式;
(2)若 、
、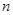 、
、 且
且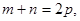 证明:
证明:
(3)若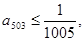 证明:
证明: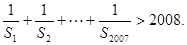
科目:gzsx 来源:2011-2012学年浙江省高三下学期3月联考理科数学 题型:填空题
下表给出一个“直角三角形数阵”
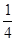
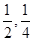
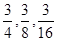
……
满足每一列成等差数列,从第三行起,每一行的数成等比数列,且各行的公比都相等,记第i行第j列的数为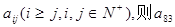 等于 ▲ .
等于 ▲ .
科目:gzsx 来源:2010-2011学年江苏省南通市高三第二次模拟考试数学试题 题型:解答题
已知数列 满足
满足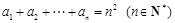 .
.
(1)求数列 的通项公式;
的通项公式;
(2)对任意给定的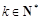 ,是否存在
,是否存在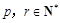 (
(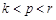 )使
)使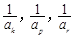 成等差数列?若存
成等差数列?若存
在,用 分别表示
分别表示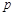 和
和 (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为 .
.