如图,已知点D,B分别在角EAF的两边,C是角EAF的内点答案解析
科目:czsx
来源:
题型:
如图,已知矩形ABCD在直线l的上方,BC在直线l上,AB=a,AD=b(a、b为常数),E是BC上
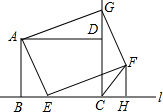
的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
(1)求证:△ADG∽△ABE;
(2)过F作FH⊥l,求证:△ADG≌△EHF;
(3)连接FC,判断当点E由B向C运动时,∠FCH的大小是否总保持不变?若∠FCH的大小不变,请用含a、b的代数式表示tan∠FCH的值;若∠FCH的大小发生改变,请举例说明.
查看答案和解析>>
科目:czsx
来源:
题型:
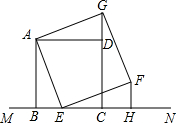
正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.
(1)判断△ADG与△ABE是否全等,并说明理由;
(2)过点F作FH⊥MN,垂足为点H,观察并猜测线段FH与线段CH的数量关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
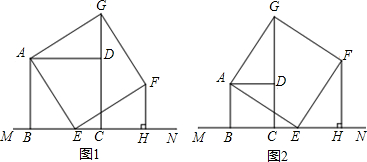
正方形四边条边都相等,四个角都是90°.如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)如图1,当点E在线段BC上(不与点B、C重合)时:
①判断△ADG与△ABE是否全等,并说明理由;
②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;
(2)如图2,当点E在射线CN上(不与点C重合)时:
①判断△ADG与△ABE是否全等,不需说明理由;
②过点F作FH⊥MN,垂足为点H,已知GD=4,求△CFH的面积.
查看答案和解析>>
科目:czsx
来源:2014届江苏吴江七年级下期期末调研数学试卷(解析版)
题型:解答题
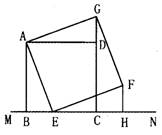
正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.
(1)判断△ADG与△ABE是否全等,并说明理由;
(2)过点F作FH⊥MN,垂足为点H,观察并猜测线段FH与线段CH的数量关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:2011-2012学年江苏吴江七年级下期期末调研数学试卷(带解析)
题型:解答题
正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.
(1)判断△ADG与△ABE是否全等,并说明理由;
(2)过点F作FH⊥MN,垂足为点H,观察并猜测线段FH与线段CH的数量关系,并说明理由.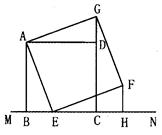
查看答案和解析>>
科目:czsx
来源:浙江省期末题
题型:解答题
正方形四边条边都相等,四个角都是90°。如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG。
(1)如图1,当点E在线段BC上(不与点B、C重合)时:
①判断△ADG与△ABE是否全等,并说明理由;
②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;
(2)如图2,当点E在射线CN上(不与点C重合)时:
①判断△ADG与△ABE是否全等,不需说明理由;
②过点F作FH⊥MN,垂足为点H,已知GD=4,求△CFH的面积。
查看答案和解析>>
科目:czsx
来源:
题型:解答题
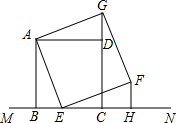 正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.
正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.
(1)判断△ADG与△ABE是否全等,并说明理由;
(2)过点F作FH⊥MN,垂足为点H,观察并猜测线段FH与线段CH的数量关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:学习周报 数学 沪科八年级版 2009-2010学年 第7期 总163期 沪科版
题型:022
如图,已知A地在B地的正南方3 km处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的距离s(单位:km)与所行驶的时间t(单位:h)之间的函数关系图象为图中的AC、BD.当他们行驶了3 h后,他们之间的距离为________km.
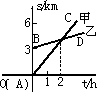
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,已知矩形ABCD在直线l的上方,BC在直线l上,AB=a,AD=b(a、b为常数),E是BC上 的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
(1)求证:△ADG∽△ABE;
(2)过F作FH⊥l,求证:△ADG≌△EHF;
(3)连接FC,判断当点E由B向C运动时,∠FCH的大小是否总保持不变?若∠FCH的大小不变,请用含a、b的代数式表示tan∠FCH的值;若∠FCH的大小发生改变,请举例说明.
查看答案和解析>>
科目:czsx
来源:四川省中考真题
题型:解答题
如图,已知点

点C在y轴的正半轴上,且

抛物线

经过

三点,其顶点为

.
求抛物线

的解析式;
(1)求抛物线的解析式
(2)试判断直线CM与以AB为直径的圆的位置关

系,并加以证明;
(3)在抛物线上是否存在点N,使得

?如果存在,那么这样的点有几个?如果不存在,请说明理由。
查看答案和解析>>
科目:czsx
来源:2011年浙江省杭州市十五中中考数学模拟试卷(3月份)(解析版)
题型:解答题
如图,已知矩形ABCD在直线l的上方,BC在直线l上,AB=a,AD=b(a、b为常数),E是BC上的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
(1)求证:△ADG∽△ABE;
(2)过F作FH⊥l,求证:△ADG≌△EHF;
(3)连接FC,判断当点E由B向C运动时,∠FCH的大小是否总保持不变?若∠FCH的大小不变,请用含a、b的代数式表示tan∠FCH的值;若∠FCH的大小发生改变,请举例说明.

查看答案和解析>>
科目:czsx
来源:2010年浙江省杭州市拱墅区中考数学二模试卷(解析版)
题型:解答题
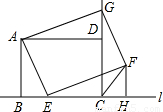
(2010•拱墅区二模)如图,已知矩形ABCD在直线l的上方,BC在直线l上,AB=a,AD=b(a、b为常数),E是BC上的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
(1)求证:△ADG∽△ABE;
(2)过F作FH⊥l,求证:△ADG≌△EHF;
(3)连接FC,判断当点E由B向C运动时,∠FCH的大小是否总保持不变?若∠FCH的大小不变,请用含a、b的代数式表示tan∠FCH的值;若∠FCH的大小发生改变,请举例说明.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的角平分线上,则轮船C在灯塔P的什么方位?
查看答案和解析>>
科目:czsx
来源:
题型:

23、如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数是否总保持不变,若∠FCN的大小保持不变,请说明理由;若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•浦东新区二模)如图,已知C岛在A岛的北偏东60°方向,在B岛的北偏西45°的方向,那么∠ACB=
105
105
度.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知正方形
ABCD在直线
MN的上方,
BC在直线
MN上,
E是
BC上一点,以
AE为边在直线
MN的上方作正方形
AEFG.

(1)连接
GD,求证:△
ADG≌△
ABE;(2)连接
FC,观察并猜测∠
FCN的度数是否总保持不变,
若∠
FCN的大小保持不变,请说明理由;
若∠
FCN的大小发生改变,请举例说明;
查看答案和解析>>
科目:czsx
来源:2012届浙江省赤城中学九年级下学期阶段测试数学卷(带解析)
题型:解答题
如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.

(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数是否总保持不变,
若∠FCN的大小保持不变,请说明理由;
若∠FCN的大小发生改变,请举例说明;
查看答案和解析>>
科目:czsx
来源:2011-2012学年浙江省九年级下学期阶段测试数学卷(解析版)
题型:解答题
如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.

(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数是否总保持不变,
若∠FCN的大小保持不变,请说明理由;
若∠FCN的大小发生改变,请举例说明;
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.

(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数是否总保持不变,
若∠FCN的大小保持不变,请说明理由;
若∠FCN的大小发生改变,请举例说明;
查看答案和解析>>

 的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上. 正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.
正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.


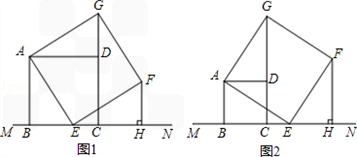
 正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.
正方形四条边都相等,四个角都是90°,如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是BC上一点,以AE为边在BC所在的直线MN的上方作正方形AEFG.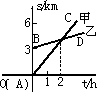
 的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上. 点C在y轴的正半轴上,且
点C在y轴的正半轴上,且 抛物线
抛物线 经过
经过 三点,其顶点为
三点,其顶点为 .
. 的解析式;
的解析式; 系,并加以证明;
系,并加以证明; ?如果存在,那么这样的点有几个?如果不存在,请说明理由。
?如果存在,那么这样的点有几个?如果不存在,请说明理由。


 如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上. 23、如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN上方作正方形AEFG.
23、如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN上方作正方形AEFG. 如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.


