科目：gzsx 来源： 题型：

若方程x²-4|x|+3=a有四个不同的解，则实数a的取值范围为

-1＜a＜3

．

查看答案和解析>>

科目：gzsx 来源：2012-2013学年福建省三明一中高一（上）第一次月考数学试卷（解析版） 题型：填空题

若方程x²-4|x|+3=a有四个不同的解，则实数a的取值范围为．

查看答案和解析>>

科目：gzsx 来源： 题型：填空题

若方程x²-4|x|+3=a有四个不同的解，则实数a的取值范围为________．

查看答案和解析>>

科目：gzsx 来源： 题型：

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数g（x）是这样定义的：当f₁（x）≥f₂（x）时，g（x）=f₁（x），当f₁（x）＜f₂（x）时，g（x）=f₂（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是（　　）

A．a＜4

B．0＜a＜4

C．0＜a＜3

D．3＜a＜4

查看答案和解析>>

科目：gzsx 来源： 题型：

对a、b∈R，记max{a，b}=

a，a≥b

b，a＜b

，设f₁（x）=|x-1|，f2(x)=-x2+6x-5，函数g（x）=max{f₁（x），f₂（x）}，若方程g（x）=a有四个不同的实数解，则实数a的取值范围是

a∈（3，4）

．

查看答案和解析>>

科目：gzsx 来源： 题型：

（2010•河西区一模）设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数g(x)=

f1(x)，f1(x)≥f2(x)

f2(x)，f1(x)＜f2(x)

，若方程g（x）=a有四个不同的实数解，则实数a的取值范围是

（3，4）

．

查看答案和解析>>

科目：gzsx 来源： 题型：

设f₁（x）=|x-1|，f2(x)=-x2+6x-5，函数g（x）是这样定义的：当f₁（x）≥f₂（x）时，g（x）=f₁（x），当f₁（x）＜f₂（x）时，g（x）=f₂（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是

（3，4）

．

查看答案和解析>>

科目：gzsx 来源：2008-2009学年重庆市江北中学高三（上）数学国庆训练3（理科）（解析版） 题型：选择题

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数g（x）是这样定义的：当f₁（x）≥f₂（x）时，g（x）=f₁（x），当f₁（x）＜f₂（x）时，g（x）=f₂（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是（）
A．a＜4
B．0＜a＜4
C．0＜a＜3
D．3＜a＜4

查看答案和解析>>

科目：gzsx 来源：2012-2013学年广东省湛江二中高三（上）第一次月考数学试卷（理科）（解析版） 题型：选择题

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数g（x）是这样定义的：当f₁（x）≥f₂（x）时，g（x）=f₁（x），当f₁（x）＜f₂（x）时，g（x）=f₂（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是（）
A．a＜4
B．0＜a＜4
C．0＜a＜3
D．3＜a＜4

查看答案和解析>>

科目：gzsx 来源：不详 题型：单选题

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数g（x）是这样定义的：当f₁（x）≥f₂（x）时，g（x）=f₁（x），当f₁（x）＜f₂（x）时，g（x）=f₂（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是（　　）

A．a＜4

B．0＜a＜4

C．0＜a＜3

D．3＜a＜4

查看答案和解析>>

科目：gzsx 来源： 题型：单选题

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数g（x）是这样定义的：当f₁（x）≥f₂（x）时，g（x）=f₁（x），当f₁（x）＜f₂（x）时，g（x）=f₂（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是

A.
a＜4
B.
0＜a＜4
C.
0＜a＜3
D.
3＜a＜4

查看答案和解析>>

科目：gzsx 来源：2010年上海市长宁区高考数学一模试卷（理科）（解析版） 题型：解答题

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数

，若方程g（x）=a有四个不同的实数解，则实数a的取值范围是．

查看答案和解析>>

科目：gzsx 来源： 题型：填空题

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数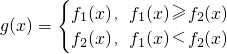 $数学公式$ ，若方程g（x）=a有四个不同的实数解，则实数a的取值范围是________．

查看答案和解析>>

科目：gzsx 来源： 题型：

填空题
（1）已知

cos2x

sin(x+

π

4

)

=

4

3

，则sin2x的值为

1

9

1

9

．
（2）已知定义在区间[0，

3π

2

]上的函数y=f（x）的图象关于直线x=

3π

4

对称，当x≥

3π

4

时，f（x）=cosx，如果关于x的方程f（x）=a有四个不同的解，则实数a的取值范围为

(-1，-

2

)

(-1，-

2

)

．

（3）设向量

a

，

b

，

c

满足

a

+

b

+

c

=

0

，(

a

-

b

)⊥

c

，

a

⊥

b

，若|

a

|=1，则|

a

|2+|

b

|2+|

c

|2的值是

4

．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知函数f（x）=|x+

1

x

|-|x-

1

x

|，若关于x的方程f（x）=2m有四个不同的实根，则实数m的取值范围是（　　）

A、（0，2）

B、（2，+∞）

C、（1，+∞）

D、（0，1）

查看答案和解析>>

科目：gzsx 来源： 题型：

已知函数f（x）=x|m-x|（x∈R），且f（4）=0，若关于x的方程f（x）=k有3个不同实根，则实数k的取值范围是（　　）

A、（0，2）

B、[2，4]

C、（0，4）

D、[0，4]

查看答案和解析>>

科目：gzsx 来源：不详 题型：解答题

填空题
（1）已知

cos2x

sin(x+

π

4

)

=

4

3

，则sin2x的值为______．
（2）已知定义在区间[0，

3π

2

]上的函数y=f（x）的图象关于直线x=

3π

4

对称，当x≥

3π

4

时，f（x）=cosx，如果关于x的方程f（x）=a有四个不同的解，则实数a的取值范围为______．

（3）设向量

a

，

b

，

c

满足

a

+

b

+

c

=

0

，(

a

-

b

)⊥

c

，

a

⊥

b

，若|

a

|=1，则|

a

|2+|

b

|2+|

c

|2的值是______．

查看答案和解析>>

科目：gzsx 来源：2011年广西南宁市高三第三次适应性测试数学试卷（理科）（解析版） 题型：选择题

已知函数f（x）=x|m-x|（x∈R），且f（4）=0，若关于x的方程f（x）=k有3个不同实根，则实数k的取值范围是（）
A．（0，2）
B．[2，4]
C．（0，4）
D．[0，4]

查看答案和解析>>

科目：gzsx 来源： 题型：单选题

已知函数f（x）=x|m-x|（x∈R），且f（4）=0，若关于x的方程f（x）=k有3个不同实根，则实数k的取值范围是

A.
（0，2）
B.
[2，4]
C.
（0，4）
D.
[0，4]

查看答案和解析>>

科目：gzsx 来源： 题型：

已知函数f（x）=

|x|

x+2

．
（1）判断函数f（x）在区间（0，+∞）上的单调性，并加以证明；
（2）如果关于x的方程f（x）=kx²有四个不同的实数解，求实数k的取值范围．

查看答案和解析>>

练习册

高中

初中

小学

方程x2-4|x|+5=m有四个不同的解，则实数m的取值范围为答案解析

若方程x²-4|x|+3=a有四个不同的解，则实数a的取值范围为________．

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数g（x）是这样定义的：当f₁（x）≥f₂（x）时，g（x）=f₁（x），当f₁（x）＜f₂（x）时，g（x）=f₂（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数 $数学公式$ ，若方程g（x）=a有四个不同的实数解，则实数a的取值范围是________．

已知函数f（x）=x|m-x|（x∈R），且f（4）=0，若关于x的方程f（x）=k有3个不同实根，则实数k的取值范围是

练习册

高中

初中

小学

方程x2-4|x|+5=m有四个不同的解，则实数m的取值范围为答案解析

若方程x2-4|x|+3=a有四个不同的解，则实数a的取值范围为________．

设f1（x）=|x-1|，f2（x）=-x2+6x-5，函数g（x）是这样定义的：当f1（x）≥f2（x）时，g（x）=f1（x），当f1（x）＜f2（x）时，g（x）=f2（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是

设f1（x）=|x-1|，f2（x）=-x2+6x-5，函数，若方程g（x）=a有四个不同的实数解，则实数a的取值范围是________．

已知函数f（x）=x|m-x|（x∈R），且f（4）=0，若关于x的方程f（x）=k有3个不同实根，则实数k的取值范围是

若方程x²-4|x|+3=a有四个不同的解，则实数a的取值范围为________．

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数g（x）是这样定义的：当f₁（x）≥f₂（x）时，g（x）=f₁（x），当f₁（x）＜f₂（x）时，g（x）=f₂（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是

设f₁（x）=|x-1|，f₂（x）=-x²+6x-5，函数 $数学公式$ ，若方程g（x）=a有四个不同的实数解，则实数a的取值范围是________．