如图在矩形ABCD点E是AD上一点且AE/ED=1/2答案解析
科目:czsx
来源:2012届浙江省九年级第二次月考数学卷
题型:解答题
.(本小题10分)
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ∽△QCP。
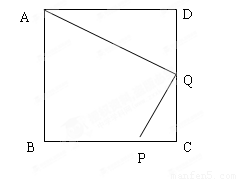
查看答案和解析>>
科目:czsx
来源:
题型:
.(本小题10分)
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ∽△QCP。

查看答案和解析>>
科目:czsx
来源:
题型:
.(本小题10分)
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ∽△QCP。
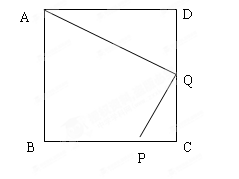
查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点。
求证:△ADQ∽△QCP。
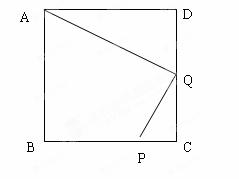
查看答案和解析>>
科目:czsx
来源:
题型:
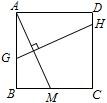
12、如图,正方形ABCD,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10cm,求GH的长.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:在平面直角坐标系中,抛物线y=ax
2-2x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-1(如图1).
(1)求该抛物线的解析式及顶点D的坐标;
(2)P是y轴上一点,若△PBC与△BOC相似,求点P的坐标;
(3)连接AD、BD(如图2),点M是AD上的一个动点,过点M作MN∥AB交BD于点N
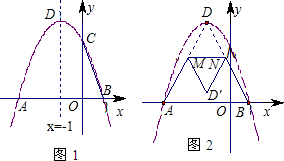
,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:

20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
(1)说明AN=MB;
(2)将△ACM绕点C按逆时针旋转180°,使A点落在CB上,请对照原题图画出符合要求的图形;
(3)在(2)所得到的图形中,结论“AN=BM”是否成立?若成立,请说明理由;若不成立,也请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

26、已知:如图,矩形ABCD中,BC延长线上一点E满足BE=BD,F是DE的中点,猜想∠AFC的度数并证明你的结论.
答:∠AFC=
90
°.
证明:
查看答案和解析>>
科目:czsx
来源:2011年浙江省嘉兴市南湖区余新中学中考数学模拟试卷(解析版)
题型:解答题
已知:在平面直角坐标系中,抛物线y=ax
2-2x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-1(如图1).
(1)求该抛物线的解析式及顶点D的坐标;
(2)P是y轴上一点,若△PBC与△BOC相似,求点P的坐标;
(3)连接AD、BD(如图2),点M是AD上的一个动点,过点M作MN∥AB交BD于点N,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.

查看答案和解析>>
科目:czsx
来源:《第23章 旋转》2012年单元测试卷(十堰七中)(解析版)
题型:解答题
如图,正方形ABCD,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10cm,求GH的长.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
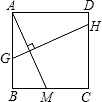 如图,正方形ABCD,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10cm,求GH的长.
如图,正方形ABCD,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10cm,求GH的长.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
(1)说明AN=MB;
(2)将△ACM绕点C按逆时针旋转180°,使A点落在CB上,请对照原题图画出符合要求的图形;
(3)在(2)所得到的图形中,结论“AN=BM”是否成立?若成立,请说明理由;若不成立,也请说明理由.
查看答案和解析>>
科目:czsx
来源:《第23章 旋转》2010年期末复习卷(解析版)
题型:解答题
如图,正方形ABCD,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10cm,求GH的长.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:在平面直角坐标系中,抛物线y=ax2-2x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-1(如图1).
(1)求该抛物线的解析式及顶点D的坐标;
(2)P是y轴上一点,若△PBC与△BOC相似,求点P的坐标;
(3)连接AD、BD(如图2),点M是AD上的一个动点,过点M作MN∥AB交BD于点N ,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
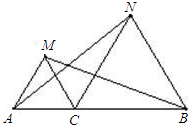 如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
(1)说明AN=MB;
(2)将△ACM绕点C按逆时针旋转180°,使A点落在CB上,请对照原题图画出符合要求的图形;
(3)在(2)所得到的图形中,结论“AN=BM”是否成立?若成立,请说明理由;若不成立,也请说明理由.
查看答案和解析>>
科目:czsx
来源:专项题
题型:解答题
如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
(1)说明AN= MB.
(2)将△ACM绕点C按逆时针旋转180°,使A点落在CB上,请对照原题图画出符合要求的图形.
(3)在(2)所得到的图形中,结论“AN=BM”是否成立,若成立,说明理由;若不成立,也请说明理由.
(4)在(2)所得到的图形中,设AM的延长线与BN相交于点D,请你判断△ABD的形状,并说明你的理由.
查看答案和解析>>
科目:czsx
来源:北京期末题
题型:解答题
已知:如图,矩形ABCD中,BC延长线上一点E满足BE=BD,F是DE的中点,猜想∠AFC的度数并证明你的结论。
查看答案和解析>>
科目:czsx
来源:新课标读想练同步测试 八年级数学(下) 人教版
题型:013
反比例函数y=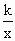 (k>0)在第一象限内的图像如图所示,点M是图像上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是
(k>0)在第一象限内的图像如图所示,点M是图像上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是
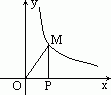
[ ]
D.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
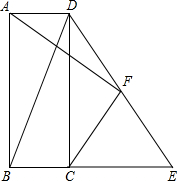 已知:如图,矩形ABCD中,BC延长线上一点E满足BE=BD,F是DE的中点,猜想∠AFC的度数并证明你的结论.
已知:如图,矩形ABCD中,BC延长线上一点E满足BE=BD,F是DE的中点,猜想∠AFC的度数并证明你的结论.
答:∠AFC=________°.
证明:
查看答案和解析>>
科目:czsx
来源:
题型:
27、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.

(1)△ACN≌△MCB吗?为什么?
(2)说明CE=CF;
(3)若△CBN绕着点C旋转一定的角度(如图2),则上述2个结论还成立吗?(此问只须写出判断结论,不要求说理)
查看答案和解析>>


 ,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.  20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.



 ,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值.
,把△DMN沿MN折叠得△D′MN,设△D′MN与△ABD的重叠部分的面积为S,请探究:S的最大值. 如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.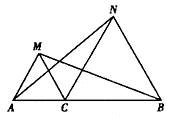
![]() (k>0)在第一象限内的图像如图所示,点M是图像上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是
(k>0)在第一象限内的图像如图所示,点M是图像上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是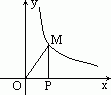
![]()
 已知:如图,矩形ABCD中,BC延长线上一点E满足BE=BD,F是DE的中点,猜想∠AFC的度数并证明你的结论.
已知:如图,矩形ABCD中,BC延长线上一点E满足BE=BD,F是DE的中点,猜想∠AFC的度数并证明你的结论.