科目：czsx 来源： 题型：
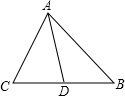如图，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm．科目：czsx 来源： 题型：
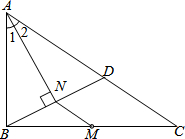（2013•永州）如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3科目：czsx 来源： 题型：
如图，AO是△ABC的中线，⊙O与AB边相切于点D．科目：czsx 来源： 题型：
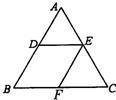3、如图，D是△ABC的边AB上的一点，过点D作DE∥BC交AC于点E，过点E作EF∥AB，交BC于点F，则图中与△ABC相似的三角形有科目：czsx 来源： 题型：
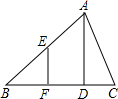如图，AD是△ABC的高，EF⊥BC，F为垂足，E是AB边的中点，DC=| 1 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
科目：czsx 来源： 题型：
| AC | BC | AB | r | L | s | |
| 图甲 | 0.6 | |||||
| 图乙 | 5.0 | 1.0 |
科目：czsx 来源： 题型：
如图，AD是△ABC的角平分线，点F，E分别在边AC，AB上，且FD=BD．
如图，D是△ABC的边AB上一点，连结CD．若AD=2，BD=6，∠ACD=∠B，求AC的长．
如图点P是△ABC的边AC上一点，∠APB=∠ABC，AP=2，CP=6 则AB=
如图，D是△ABC的边AB上一点．请添加一个条件：
8、如图，DE是△ABC中边AC的垂直平分线，若BC=18cm，AB=10cm，则△ABD的周长为（ ）
15、如图，D是△ABC的边AB上一点，要使△BCD∽△BAC，只需添加条件为
如图，D是△ABC的边BC上的一点，AB=2，BD=1，DC=3，求证：△ABD∽△CBA．
23、如图，D是△ABC的边AB上一点，DF交AC于点E，DE=FE，FC∥AB，求证：△ADE≌△CFE．
12、如图，D是△ABC的边AB上的点，请你添加一个条件，使△ACD与△ABC相似，你添加的条件是
如图，D是△ABC的边BC的中点，DE⊥AC，DF⊥AB，垂足分别为E、F，且DE=DF．试判断△ABC的形状，并给出证明．
6、如图，M是△ABC的边BC的中点，AN平分∠BAC，且BN⊥AN，垂足为N，且AB=6，BC=10，MN=1.5，则△ABC的周长是（ ）
（2013•聊城）如图，D是△ABC的边BC上一点，已知AB=4，AD=2．∠DAC=∠B，若△ABD的面积为a，则△ACD的面积为（ ）
19、如图，D是△ABC的边AC上一点，若AB=AC，要使△CDB∽△BAC，只需添加条件