对于任意实数a,b,都有a+b=a(a-b)+1,等式右边式通常的加法“答案解析
科目:czsx
来源:
题型:
定义新运算:
对于任意实数a、b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,求(-2)⊕3的值.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•河北)定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:
2⊕5=2×(2-5)+1
=2×(-3)+1
=-6+1
=-5
(1)求(-2)⊕3的值;
(2)若3⊕x的值小于13,求x的取值范围,并在图所示的数轴上表示出来.

查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(河北卷)数学(解析版)
题型:解答题
定义新运算:对于任意实数a,b,都有a?b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2?5=2´(2-5)+1=2´(-3)+1=-6+1=-5.
(1)求(-2)?3的值
(2)若3?x的值小于13,求x的取值范围,并在图示的数轴上表示出来.

查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(河北卷)数学(带解析)
题型:解答题
定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2⊕5=2´(2-5)+1=2´(-3)+1=-6+1=-5.
(1)求(-2)⊕3的值
(2)若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
定义新运算:对于任意实数a、b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,求(-2)⊕3的值.
查看答案和解析>>
科目:czsx
来源:2013年河北市高级中等学校招生考试数学
题型:044
定义新运算:对于任意实数a,b,都有a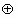 b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2
b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2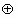 5=2×(2-5)+1
5=2×(2-5)+1
=2´
(-3)+1
=-6+1
=-5
(1)求(-2)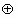 3的值
3的值
(2)若3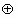 x的值小于13,求x的取值范围,并在下图所示的数轴上表示出来.
x的值小于13,求x的取值范围,并在下图所示的数轴上表示出来.
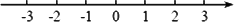
查看答案和解析>>
科目:czsx
来源:
题型:解答题
定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:
2⊕5=2×(2-5)+1
=2×(-3)+1
=-6+1
=-5
(1)求(-2)⊕3的值;
(2)若3⊕x的值小于13,求x的取值范围,并在图所示的数轴上表示出来.

查看答案和解析>>
科目:czsx
来源:2013年河北省中考数学试卷(解析版)
题型:解答题
定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:
2⊕5=2×(2-5)+1
=2×(-3)+1
=-6+1
=-5
(1)求(-2)⊕3的值;
(2)若3⊕x的值小于13,求x的取值范围,并在图所示的数轴上表示出来.
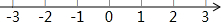
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•金平区模拟)现定义运算“★”,对于任意实数a、b,都有a★b=a2-6a+b,如:3★5=32-6×3+5,若x★2=9,则实数x的值是( )
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•平凉)现定义运算“★”,对于任意实数a、b,都有a★b=a
2-3a+b,如:3★5=3
2-3×3+5,若x★2=6,则实数x的值是
-1或4
-1或4
.
查看答案和解析>>
科目:czsx
来源:
题型:
对于任意实数a,b,c,d,定义有序实数对(a,b)与(c,d)之间的运算“△”为:(a,b)△(c,d)=(ac+bd,ad+bc).如果对于任意实数u,v,都有(u,v)△(x,y)=(u,v),那么(x,y)为( )
查看答案和解析>>
科目:czsx
来源:
题型:
9、用“
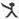
”、“

”定义新运算:对于任意实数a,b,都有a

b=a 和 a
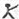
b=b,例如3
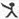
2=3,3

2=2.则(2006
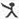
2005)
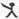
(2004

2003)=( )
查看答案和解析>>
科目:czsx
来源:
题型:
18、用“
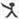
”、“
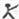
”定义新运算:对于任意实数a,b,都有a

b=a和a
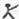
b=b,例如3
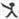
2=3,3
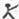
2=2.则(2006
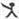
2005)
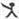
(2004
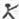
2003)=
2006
.
查看答案和解析>>
科目:czsx
来源:
题型:
4、如果我们用“♀”、“♂”来定义新运算:对于任意实数a,b,都有a♀b=a,a♂b=b,例如3♀2=3,3♂2=2.则(仙♀市)♀(中♂学)=
仙
.
查看答案和解析>>
科目:czsx
来源:
题型:
10、用“

”、“
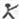
”定义新运算:对于任意实数a,b,都有a
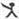
b=a和a
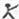
b=b,例如3
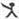
2=3,3
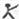
2=2.则(2010
2009)
(2007
2008)的值是( )
查看答案和解析>>
科目:czsx
来源:
题型:
用“☆”定义新运算:对于任意实数a、b,都有a☆b=b
2+a.例如2☆3=3
2+2=11,那么(-8)☆3=
67
67
.
查看答案和解析>>
科目:czsx
来源:
题型:
18、如果我们用“♀”、“♂”来定义新运算:对于任意实数a,b,都有a♀b=a,a♂b=b,例如3♀2=3,3♂2=2.则(勐♀捧)♀(中♂学)=
勐
.
查看答案和解析>>
科目:czsx
来源:
题型:
(2010•资阳)给出下列命题:
①若方程x
2+5x-6=0的两根分别为x
1,x
2,则
+=;
②对于任意实数x、y,都有(x-y)(x
2+xy+y
2)=x
3-y
3;
③如果一列数3,7,11,…满足条件:“以3为第一个数,从第二个数开始每一个数与它前面相邻的数的差为4”,那么99不是这列数中的一个数;
④若※表示一种运算,且1※2=1,3※2=7,4※4=8,…,按此规律,则可能有a※b=3a-b.
其中所有正确命题的序号是
①②④
①②④
.
查看答案和解析>>
科目:czsx
来源:
题型:
用“※”定义新运算:对于任意实数a、b,都有a※b=2a
2+b.例如3※4=2×3
2+4=22,那么(-5)※(-8)=
42
42
.
查看答案和解析>>
科目:czsx
来源:
题型:
用“«”“»”定义新运算:对于任意实数a,b,都有a«b=a,和a»b=b,例如:3«2=3,3»2=2,则(2012»2011)«(2010»2009)=
2011
2011
.
查看答案和解析>>




![]() b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2
b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2![]() 5=2×(2-5)+1
5=2×(2-5)+1![]() 3的值
3的值![]() x的值小于13,求x的取值范围,并在下图所示的数轴上表示出来.
x的值小于13,求x的取值范围,并在下图所示的数轴上表示出来.
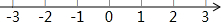
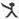 ”、“
”、“ ”定义新运算:对于任意实数a,b,都有a
”定义新运算:对于任意实数a,b,都有a b=a 和 a
b=a 和 a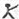 b=b,例如3
b=b,例如3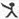 2=3,3
2=3,3 2=2.则(2006
2=2.则(2006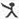 2005)
2005)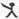 (2004
(2004 2003)=( )
2003)=( )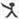 ”、“
”、“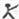 ”定义新运算:对于任意实数a,b,都有a
”定义新运算:对于任意实数a,b,都有a b=a和a
b=a和a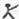 b=b,例如3
b=b,例如3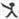 2=3,3
2=3,3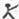 2=2.则(2006
2=2.则(2006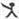 2005)
2005)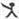 (2004
(2004 2003)=
2003)= ”、“
”、“ ”定义新运算:对于任意实数a,b,都有a
”定义新运算:对于任意实数a,b,都有a b=a和a
b=a和a b=b,例如3
b=b,例如3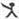 2=3,3
2=3,3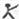 2=2.则(2010
2=2.则(2010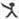 2009)
2009)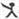 (2007
(2007 2008)的值是( )
2008)的值是( )