如图,在△ABC中,∠ACB=90°,∠B=45°,且AC=BC答案解析
科目:czsx
来源:
题型:

(2012•塘沽区二模)如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是
18
18
.
查看答案和解析>>
科目:czsx
来源:
题型:
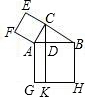
如图,在△ABC中,∠ACB=90°,分别以AC,AB为边,在△ABC外作正方形ACEF和正方形AGHB,作CK⊥AB,分别交AB和GH于D和K,则正方形ACEF的面积S
1与矩形AGKD的面积S
2的大小关系是( )
| A、S1=S2 |
| B、S1>S2 |
| C、S1<S2 |
| D、不能确定,与的大小有关 |
查看答案和解析>>
科目:czsx
来源:
题型:
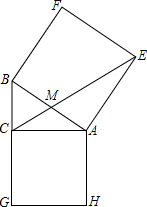
如图,在△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形AEFB和正方形ACGH,连接CE.试说明:三角形AEC的面积等于正方形ACGH面积的一半.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
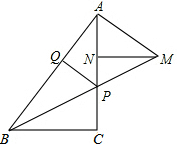
如图,在△ABC中,∠ACB=90゜,P为AC上一点,PQ⊥AB于Q,AM⊥AB交BP的延长线于M,MN⊥AC于N,AQ=MN.
(1)求证:AP=AM;
(2)求证:PC=AN.
查看答案和解析>>
科目:czsx
来源:不详
题型:单选题
如图,在△ABC中,∠ACB=90°,分别以AC,AB为边,在△ABC外作正方形ACEF和正方形AGHB,作CK⊥AB,分别交AB和GH于D和K,则正方形ACEF的面积S
1与矩形AGKD的面积S
2的大小关系是( )
| A.S1=S2 |
| B.S1>S2 |
| C.S1<S2 |
| D.不能确定,与的大小有关 |
查看答案和解析>>
科目:czsx
来源:
题型:解答题
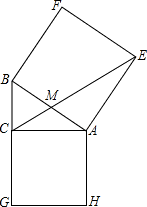 如图,在△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形AEFB和正方形ACGH,连接CE.试说明:三角形AEC的面积等于正方形ACGH面积的一半.
如图,在△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形AEFB和正方形ACGH,连接CE.试说明:三角形AEC的面积等于正方形ACGH面积的一半.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
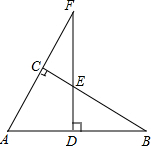 如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.
如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
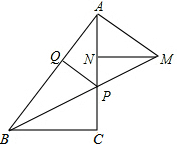 如图,在△ABC中,∠ACB=90゜,P为AC上一点,PQ⊥AB于Q,AM⊥AB交BP的延长线于M,MN⊥AC于N,AQ=MN.
如图,在△ABC中,∠ACB=90゜,P为AC上一点,PQ⊥AB于Q,AM⊥AB交BP的延长线于M,MN⊥AC于N,AQ=MN.
(1)求证:AP=AM;
(2)求证:PC=AN.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
 如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是________.
如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是________.
查看答案和解析>>
科目:czsx
来源:
题型:单选题
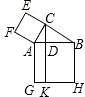 如图,在△ABC中,∠ACB=90°,分别以AC,AB为边,在△ABC外作正方形ACEF和正方形AGHB,作CK⊥AB,分别交AB和GH于D和K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是
如图,在△ABC中,∠ACB=90°,分别以AC,AB为边,在△ABC外作正方形ACEF和正方形AGHB,作CK⊥AB,分别交AB和GH于D和K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是
- A.
S1=S2
- B.
S1>S2
- C.
S1<S2
- D.
不能确定,与
的大小有关
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F.
(1)求DC的长和旋转的角度n;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
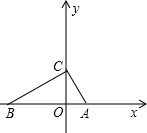
如图,在△ABC中,∠ACB=90°,AC=
2,斜边AB在x轴上,点C在y轴的正半轴上,点A的坐标为(2,0).则直角边BC所在直线的解析式为
.
查看答案和解析>>
科目:czsx
来源:
题型:
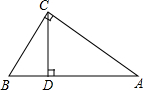
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,求证:AD=3BD.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在△ABC中,∠ACB=90°AC=BC=6cm,正方形DEFG的边长为2cm,其一边EF在BC所在的直线L上,开始时点F与点C重合,让正方形DEFG沿直线L向右以每秒
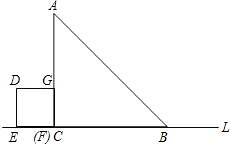
1cm的速度作匀速运动,最后点E与点B重合.
(1)请直接写出该正方形运动6秒时与△ABC重叠部分面积的大小;
(2)设运动时间为x(秒),运动过程中正方形DEFG与△ABC重叠部分的面积为y(cm
2).
①在该正方形运动6秒后至运动停止前这段时间内,求y与x之间的函数关系式;
②在该正方形整个运动过程中,求当x为何值时,y=
.
查看答案和解析>>
科目:czsx
来源:
题型:
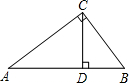
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°,则下列结论中正确的是( )
查看答案和解析>>
科目:czsx
来源:
题型:
(1)计算:
|-2|-(2-π)0+()-1+(-2)3;
(2)先将:
(1+)÷ 化简,然后请自选一个你喜欢的x值,再求原式的值;
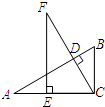
(3)已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.求证:AB=FC.
查看答案和解析>>
科目:czsx
来源:
题型:
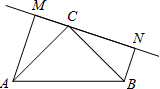
如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.求证:△MAC≌△NCB.
查看答案和解析>>
科目:czsx
来源:
题型:
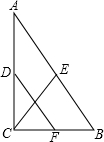
已知:如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.求证:CF=DE.
查看答案和解析>>

 (2012•塘沽区二模)如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是
(2012•塘沽区二模)如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是 如图,在△ABC中,∠ACB=90°,分别以AC,AB为边,在△ABC外作正方形ACEF和正方形AGHB,作CK⊥AB,分别交AB和GH于D和K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是( )
如图,在△ABC中,∠ACB=90°,分别以AC,AB为边,在△ABC外作正方形ACEF和正方形AGHB,作CK⊥AB,分别交AB和GH于D和K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是( ) 如图,在△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形AEFB和正方形ACGH,连接CE.试说明:三角形AEC的面积等于正方形ACGH面积的一半.
如图,在△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形AEFB和正方形ACGH,连接CE.试说明:三角形AEC的面积等于正方形ACGH面积的一半.  如图,在△ABC中,∠ACB=90゜,P为AC上一点,PQ⊥AB于Q,AM⊥AB交BP的延长线于M,MN⊥AC于N,AQ=MN.
如图,在△ABC中,∠ACB=90゜,P为AC上一点,PQ⊥AB于Q,AM⊥AB交BP的延长线于M,MN⊥AC于N,AQ=MN.
 如图,在△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形AEFB和正方形ACGH,连接CE.试说明:三角形AEC的面积等于正方形ACGH面积的一半.
如图,在△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形AEFB和正方形ACGH,连接CE.试说明:三角形AEC的面积等于正方形ACGH面积的一半. 如图,在△ABC中,∠ACB=90゜,P为AC上一点,PQ⊥AB于Q,AM⊥AB交BP的延长线于M,MN⊥AC于N,AQ=MN.
如图,在△ABC中,∠ACB=90゜,P为AC上一点,PQ⊥AB于Q,AM⊥AB交BP的延长线于M,MN⊥AC于N,AQ=MN. 如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是________.
如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是________. 如图,在△ABC中,∠ACB=90°,分别以AC,AB为边,在△ABC外作正方形ACEF和正方形AGHB,作CK⊥AB,分别交AB和GH于D和K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是
如图,在△ABC中,∠ACB=90°,分别以AC,AB为边,在△ABC外作正方形ACEF和正方形AGHB,作CK⊥AB,分别交AB和GH于D和K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是 的大小有关
的大小有关 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F.
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F. 如图,在△ABC中,∠ACB=90°,AC=2
如图,在△ABC中,∠ACB=90°,AC=2 1cm的速度作匀速运动,最后点E与点B重合.
1cm的速度作匀速运动,最后点E与点B重合. (1)计算:|-2|-(2-π)0+(
(1)计算:|-2|-(2-π)0+(