
科目:gzsx 来源: 题型:
| 1 | bnbn+2 |
科目:gzsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
科目:gzsx 来源: 题型:
| 1 |
| cn |
| 1 |
| 5 |
科目:gzsx 来源: 题型:
| 1 | bnbn+2 |
科目:gzsx 来源: 题型:
| an-1 |
| an |
| an-1+1 |
| 1-an |
| 1 |
| an |
科目:gzsx 来源: 题型:
| 1 | bnbn+1 |
科目:gzsx 来源: 题型:
 下列关于星星的图案构成一个数列{an},an(n∈N*)对应图中星星的个数
下列关于星星的图案构成一个数列{an},an(n∈N*)对应图中星星的个数| 1 |
| an |
| 2n2-9n-11 |
| 2n |
科目:gzsx 来源: 题型:
| 1 |
| anan+1 |
| c1 |
| b1 |
| c2 |
| b2 |
| c3 |
| b3 |
| cn |
| bn |
科目:gzsx 来源:2010年河南省周口市高二上学期期中考试数学卷 题型:解答题
在数列{an}中,a1=2,a4=8,且满足an+2=2an+1-an(n∈N*)
(1)求数列{an}的通项公式
(2)设bn=2n-1·an,求数列{bn}的前n项和sn
科目:gzsx 来源:2011年河南省卫辉市第一中学高二上学期末文科数学卷 题型:解答题
在数列{an}中,a1=2,a4=8,且满足an+2=2an+1-an(n∈N*)
(1)求数列{an}的通项公式
(2)设bn=2n-1·an,求数列{bn}的前n项和sn
科目:gzsx 来源:2010年河南省周口市高二上学期期中考试数学卷 题型:解答题
在数列{an}中,a1=2,a4=8,且满足an+2=2an+1-an(n∈N*)
(1)求数列{an}的通项公式
(2)设bn=2n-1·an,求数列{bn}的前n项和sn
科目:gzsx 来源:2011届山东省济宁一中高三第三次月考文科数学卷 题型:解答题
(满分12分)已知等差数列 ,a2=9,a5=21
,a2=9,a5=21
(1)数列{an}的通项公式
(2)设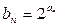 ,求数列{bn}的前n项和Sn。
,求数列{bn}的前n项和Sn。
科目:gzsx 来源:2010-2011学年山东省高三第三次月考文科数学卷 题型:解答题
(满分12分)已知等差数列 ,a2=9,a5=21
,a2=9,a5=21
(1)数列{an}的通项公式
(2)设 ,求数列{bn}的前n项和Sn。
,求数列{bn}的前n项和Sn。
科目:gzsx 来源: 题型:解答题
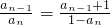 (n∈N*,n>1).
(n∈N*,n>1).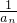 是等差数列;
是等差数列;科目:gzsx 来源:数学教研室 题型:044
(1)求数列{bn}的通项公式;
(2)求数列{bn}的前n项和Sn的公式;
(3)设Pn=b1+b4+b7+…+b3n-2,Qn=b10+b12+b14+…+b2n+8,其中n=1,2,…,试比较Pn与Qn的大小,并证明你的结论.
科目:gzsx 来源:数学教研室 题型:044
(1)求数列{bn}的通项公式;
(2)求数列{bn}的前n项和Sn的公式;
(3)设Pn=b1+b4+b7+…+b3n-2,Qn=b10+b12+b14+…+b2n+8,其中n=1,2,…,试比较Pn与Qn的大小,并证明你的结论.
科目:gzsx 来源: 题型:044
已知{an}是等比数列,a1=2,a3=18;{bn}是等差数列,b1=2,b1+b2+b3+b4=a1+a2+a3>20.
(1)求数列{bn}的通项公式;
(2)求数列{bn}的前n项和Sn的公式;
(3)设Pn=b1+b4+b7+…+b3n-2,Qn=b10+b12+b14+…+b2n+8,其中n=1,2,…,试比较Pn与Qn的大小,并证明你的结论.
科目:gzsx 来源: 题型:
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设![]() 求数列{bn}的前n项和Sn;
求数列{bn}的前n项和Sn;
(Ⅲ)若0<an<1对任意![]() N*成立,证明0<c
N*成立,证明0<c![]() 1.
1.
科目:gzsx 来源:不详 题型:解答题
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |