练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知椭圆C： x2 a2 + y2 b2 =1（a＞b＞0）的离心率为 2 2 ，且椭圆C上一点与两个焦点F1，F2构成的三角形的周长为2 2 +2．

    已知椭圆C： x2 a2 + y2 b2 =1（a＞b＞0）的离心率为 2 2 ，且椭圆C上一点与两个焦点F1，F2构成的三角形的周长为2 2 +2．答案解析

    科目：gzsx 来源：不详 题型：单选题

    已知幂函数y=xn（n=-1，2，3）和椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）有8个不同的交点，分别为Ai（i=1，2，…，8），F点是椭圆C的右焦点，则8条不同线段AiF（i=1，2，…，8）中所有两条线段之和最多有（　　）个不同的值．
    A．28 B．25 C．24 D．20

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C：
    x
    2
     
    a
    2
     
    +
    y
    2
     
    b
    2
     
    =1(a＞b＞0)    ．
    （1）若椭圆的长轴长为4，离心率为
    		3
    2
    ，求椭圆的标准方程；
    （2）在（1）的条件下，设过定点M（0，2）的直线l与椭圆C交于不同的两点A、B，且∠AOB为锐角（其中O为坐标原点），求直线l的斜率k的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C：
    x
    2
     
    a
    2
     
    +
    y
    2
     
    b
    2
     
    =1(a＞b＞0)    ，F1、F2分别为椭圆c的左右焦点，点P在椭圆C上（不是顶点），△PF1F2内一点G满足3
    PG
    =
    PF1
    +
    PF2
    ，其中
    OG
    =(
    1
    9
    a，
    		6
    9
    a)    ．
    （I）求椭圆C的离心率；
    （Ⅱ）若椭圆C短轴长为2
    		3
    ，过焦点F2的直线l与椭圆C相交于A、B两点（A、B不是左右顶点），若
    AF2
    =2
    F2B
    ，求△F1AB面积．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C：
    x
    2
     
    a
    2
     
    +
    y
    2
     
    b
    2
     
    =1(a＞b＞0)    ，点P(b，
    a
    2
    )    在椭圆上，其左、右焦点为F1、F2．
    （Ⅰ）求椭圆C的离心率；
    （Ⅱ）若
    PF1
    •
    PF2
    =
    1
    2
    ，过点S(0，-
    1
    3
    )    的动直线l交椭圆于A、B两点，请问在y轴上是否存在定点M，使以AB为直径的圆恒过这个定点？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•枣庄二模）已知椭圆C：
    x
    2
     
    a
    2
     
    +
    y
    2
     
    b
    2
     
    =1(a＞b＞0)    的左顶点为A，右焦点为F，且过点（1，
    3
    2
    ），椭圆C的焦点与曲线2
    x
    2
     
    -2
    y
    2
     
    =1    的焦点重合．
    （1）求椭圆C的方程；
    （2）过点F任作椭圆C的一条弦PQ，直线AP、AQ分别交直线x=4于M、N两点，点M、N的纵坐标分别为m、n．请问以线段MN为直径的圆是否经过x轴上的定点？若存在，求出定点的坐标，并证明你的结论；若不存在，请说明理由．
    （3）在（2）问的条件下，求以线段MN为直径的圆的面积的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C：
    x
    2
     
    a
    2
     
    +
    y
    2
     
    b
    2
     
    =1(a＞b＞0)    经过 点B(0，
    		3
    )    ，且离心率为
    1
    2
    ，右顶点为A，左右焦点分别为F1，F2；椭圆C2以坐标原点为中心，且以F1F2为短轴端，上顶点为D．
    （Ⅰ）求椭圆C1的方程；
    （Ⅱ）若C1与C2交于M、N、P、Q四点，当AD∥F2B时，求四边形MNPQ的面积．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•安徽模拟）已知椭圆C：
    x
    2
     
    a
    2
     
    +
    y
    2
     
    b
    2
     
    =1(a＞b＞0)    的两个焦点分别为F1（-1，0），F2（1，0），长半轴长为
    		2
    ．
    （1）（i）求椭圆C的方程；
    （ii）类比结论“过圆
    x
    2
     
    +
    y
    2
     
    =r2    上任一点（x0，y0）的切线方程是x0x+yy0=
    r
    2
     
    ”，归纳得出：过椭圆
    x
    2
     
    a
    2
     
    +
    y
    2
     
    b
    2
     
    =1(a＞b＞0)    上任一点（x0，y0）的切线方程是
    x0x
    a
    2
     
    +
    y0y
    b
    2
     
    =1
    x0x
    a
    2
     
    +
    y0y
    b
    2
     
    =1
    ；
    （2）设M，N是直线x=2上的两个点，若
    F1M
    •
    F2M
    =0，求|MN|    的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•枣庄二模）已知椭圆C：
    x
    2
     
    a
    2
     
    +
    y
    2
     
    b
    2
     
    =1(a＞b＞0)    的左顶点为A，右焦点为F，且过点（1，
    3
    2
    ），椭圆C的焦点与曲线2
    x
    2
     
    -2
    y
    2
     
    =1    的焦点重合．
    （1）求椭圆C的方程；
    （2）过点F任作椭圆C的一条弦PQ，直线AP、AQ分别交直线x=4于M、N两点，点M、N的纵坐标分别为m、n．请问以线段MN为直径的圆是否经过x轴上的定点？若存在，求出定意的坐标，并证明你的结论；若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C的方程是
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0），斜率为1的直线l与椭圆C交于A（x1，y1），B（x2，y2）两点．
    （Ⅰ）若椭圆的离心率e=
    		3
    2
    ，直线l过点M（b，0），且
    OA
    •
    OB
    =
    32
    5
    cot∠AOB    ，求椭圆的方程；
    （Ⅱ）直线l过椭圆的右焦点F，设向量
    OP
    =λ(
    OA
    +
    OB
    )    （λ＞0），若点P在椭圆C上，求λ的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C的方程为
    x2
    a2
    + 
    y2
    b2
    =1    （a＞b＞0），称圆心在坐标原点O，半径为
    		a2+b2
    的圆为椭圆C的“伴随圆”，椭圆C的短轴长为2，离心率为
    		6
    3
    ．
    （Ⅰ）求椭圆C及其“伴随圆”的方程；
    （Ⅱ）若直线l与椭圆C交于A，B两点，与其“伴随圆”交于C，D两点，当|CD|=
    		13
     时，求△AOB面积的最大值．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    已知椭圆C的方程为
    x2
    a2
    + 
    y2
    b2
    =1    （a＞b＞0），称圆心在坐标原点O，半径为
    		a2+b2
    的圆为椭圆C的“伴随圆”，椭圆C的短轴长为2，离心率为
    		6
    3
    ．
    （Ⅰ）求椭圆C及其“伴随圆”的方程；
    （Ⅱ）若直线l与椭圆C交于A，B两点，与其“伴随圆”交于C，D两点，当|CD|=
    		13
     时，求△AOB面积的最大值．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：单选题

    椭圆
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的左、右焦点分别是F1F2，过F2作倾斜角为120°的直线与椭圆的一个交点为M，若MF1垂直于x轴，则椭圆的离心率为（　　）
    A．
    12-2
    		3
    11
    		 B．2-
    		3
    		 C．2（2-
    		3
    ）    		 D．
    		3
    3

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2007•河北区一模）已知椭圆C的方程为 
    x2
    a2
    +
    y2
    b2
    =1     （a＞b＞0），过其左焦点F1（-1，0）斜率为1的直线交椭圆于P、Q两点．
    （Ⅰ）若
    OP
    +
    OQ
    与
    a
    =（-3，1）共线，求椭圆C的方程；
    （Ⅱ）已知直线l：x+y-
    1
    2
    =0，在l上求一点M，使以椭圆的焦点为焦点且过M点的双曲线E的实轴最长，求点M的坐标和此双曲线E的方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•衡阳模拟）已知椭圆C的方程为
    y2
    a2
    +
    x2
    b2
    =1（a＞b＞0），离心率e=
    		2
    2
    ，上焦点到直线y=
    a2
    c
    的距离为
    		2
    2
    ，直线l与y轴交于一点P（0，m），与椭圆C交于相异两点A，B且
    AP
    =t
    PB
    ．
    （1）求椭圆C的方程；
    （2）若
    OA
    +t
    OB
    =4
    OP
    ，求m的取值范围•

    查看答案和解析>>

    科目：gzsx 来源： 题型：

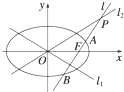
    精英家教网已知椭圆C的方程为
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0），双曲线
    x2
    a2
    -
    y2
    b2
    =1的两条渐近线为l1、l2，过椭圆C的右焦点F作直线l，使l⊥l1，又l与l2交于P点，设l与椭圆C的两个交点由上至下依次为A、B．（如图）
    （1）当l1与l2夹角为60°，双曲线的焦距为4时，求椭圆C的方程；
    （2）当
    FA
    =λ
    AP
    时，求λ的最大值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （1）求右焦点坐标是（2，0），且经过点( -2 ， -
    		2
     )    的椭圆的标准方程；
    （2）已知椭圆C的方程是
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）．设斜率为k的直线l，交椭圆C于A、B两点，AB的中点为M．证明：当直线l平行移动时，动点M在一条过原点的定直线上．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆C：M：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的离心率e=
    3
    5
    ，且椭圆上一点与椭圆的两个焦点构成的三角形周长为16
    （Ⅰ）求椭圆M的方程；
    （Ⅱ）若O（0，0）、P（2，2），试探究在椭圆C内部是否存在整点Q（平面内横、纵坐标均为整数的点称为整点），使得△OPQ的面积S△OPQ=4？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2011•洛阳二模）已知椭圆C的方程为
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0），F1（-2，0）为左焦点，点M（
    		2
    ，
    		3
    ）在椭圆上．
    （1）求椭圆C的方程；
    （2）过点F1作两条斜率存在且互相垂直的直线l1，l2，设L3与椭圆C相交于点A，B．l2 与椭圆C相交于点D．E，求
    AD
    •
    EB
    的最小值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网已知椭圆C的方程是
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0），点A，B分别是椭圆的长轴的左、右端点，
    左焦点坐标为（-4，0），且过点P ( 
    3
    2
    ，  
    5
    2
    		3
    )    ．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）已知F是椭圆C的右焦点，以AF为直径的圆记为圆M，试问：过P点能否引圆M的切线，若能，求出这条切线与x轴及圆M的弦PF所对的劣弧围成的图形的面积；若不能，说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网（1）求右焦点坐标是（2，0），且经过点（-2，-
    		2
    ）的椭圆的标准方程．
    （2）已知椭圆C的方程是
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）．设斜率为k的直线l交椭圆C于A、B两点，AB的中点为M．证明：当直线l平行移动时，动点M在一条过原点的定直线上．
    （3）利用（2）所揭示的椭圆几何性质，用作图方法找出下面给定椭圆的中心，简要写出作图步骤，并在图中标出椭圆的中心．

    查看答案和解析>>