若直线x+y+m=0（m＞0）与圆x^2+y^2=2交于不同的两点A、B，O是坐标原点答案及详细解析过程——青夏教育精英家教网—

科目：gzsx 来源： 题型：

设点P是圆x²+y²=4上任意一点，由点P向x轴作垂线PP₀，垂足为P_o，且

MP0

=

3

2

pp0

．
（Ⅰ）求点M的轨迹C的方程；
（Ⅱ）设直线l：y=kx+m（m≠0）与（Ⅰ）中的轨迹C交于不同的两点A，B．
（1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；
（2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线l过定点（Q点除外），并求出该定点的坐标．

查看答案和解析>>

科目：gzsx 来源：不详 题型：解答题

设点P是圆x²+y²=4上任意一点，由点P向x轴作垂线PP₀，垂足为P_o，且

MP0

=

3

2

pp0

．
（Ⅰ）求点M的轨迹C的方程；
（Ⅱ）设直线l：y=kx+m（m≠0）与（Ⅰ）中的轨迹C交于不同的两点A，B．
（1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；
（2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线l过定点（Q点除外），并求出该定点的坐标．

查看答案和解析>>

科目：gzsx 来源：2012-2013学年湖北省高三（上）期末数学试卷（理科）（解析版） 题型：解答题

设点P是圆x²+y²=4上任意一点，由点P向x轴作垂线PP，垂足为P_o，且

=

．
（Ⅰ）求点M的轨迹C的方程；
（Ⅱ）设直线l：y=kx+m（m≠0）与（Ⅰ）中的轨迹C交于不同的两点A，B．
（1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；
（2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线l过定点（Q点除外），并求出该定点的坐标．

查看答案和解析>>

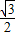
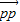科目：gzsx 来源： 题型：

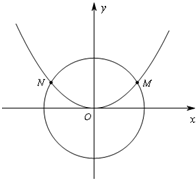如图，已知抛物线C₁：x²=2py（p＞0）与圆C2：x2+y2=

16

9

交于M、N两点，
且∠MON=120°．
（Ⅰ）求抛物线C₁的方程；
（Ⅱ）设直线l与圆C₂相切．
（ⅰ）若直线l与抛物线C₁也相切，求直线l的方程；
（ⅱ）若直线l与抛物线C₁交与不同的A、B两点，求

OA

•

OB

的取值范围．

查看答案和解析>>

科目：gzsx 来源：山东省潍坊市重点中学2012届高三2月月考数学理科试题 题型：022

下列5个命题：

(1)函数y＝cosx－sinx的图象向左平移个单位，所得函数图象关于原点对称；

(2)若命题p：“存在x∈R，x²－x－1＞0”，则命题p的否定为：“任意x∈R，x²－x－1≤0”；

(3)函数f(x)＝logx＋x²－3的零点有2个；

(4)函数在x＝1＋处取最小值；

(5)已知直线x－y＋a＝0与圆x²＋y²＝1交于不同两点A、B，O为坐标原点，则“a＝1”是“向量、满足|＋|＝|－|”的充分不必要条件．

其中所有正确命题的序号是________．

查看答案和解析>>

科目：gzsx 来源：山东省潍坊市重点中学2012届高三2月月考数学文科试题 题型：022

下列5个命题：

(1)函数y＝cosx－sinx的图象向左平移个单位，所得函数图象关于原点对称；

(2)若命题p：“存在x∈R，x²－x－1＞0”，则命题p的否定为：“任意x∈R，x²－x－1≤0”；

(3)函数f(x)＝logx＋x²－3的零点有2个；

(4)函数在x＝1＋处取最小值；

(5)已知直线x－y＋a＝0与圆x²＋y²＝1交于不同两点A、B，O为坐标原点，则“a＝1”是“向量、满足|＋|＝|－|”的充分不必要条件．

其中所有正确命题的序号是________．

查看答案和解析>>

科目：gzsx 来源：浙江省温州中学2010-2011学年高一下学期期末考试数学试题 题型：013

直线x＋y＝a与圆x²＋y²＝1交于不同的两点A，B，O为坐标原点，若，则a的值为

[　　]

A．

B．

C．

D．

查看答案和解析>>

科目：gzsx 来源：学习高手必修二数学苏教版苏教版 题型：044

已知实数A、B、C满足A²＋B²＝2C²≠0，求证：直线Ax＋By＋C＝0与圆x²＋y²＝1交于不同的两点P、Q，并求弦PQ的长．

查看答案和解析>>

科目：gzsx 来源：导学大课堂必修二数学苏教版苏教版 题型：044

已知实数A、B、C满足A²＋B²＝2C²≠0，求证：直线Ax＋By＋C＝0与圆x²＋y²＝1交于不同的两点P、Q，并求弦PQ的长．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知动点M到点F（-

2

，0）的距离与到直线x=-

2

的距离之比为

2

．
（1）求动点M的轨迹C的方程；
（2）若过点E（0，1）的直线与曲线C在y轴左侧交于不同的两点A、B，点P（-2，0）满足

PN

=

1

2

(

PA

+

PB

)，求直线PN在y轴上的截距d的取值范围．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知动圆C过点A（-2，0），且与圆M：（x-2）²+y²=64相内切
（1）求动圆C的圆心的轨迹方程；
（2）设直线l：y=kx+m（其中k，m∈Z）与（1）所求轨迹交于不同两点B，D，与双曲线

x2

4

-

y2

12

=1交于不同两点E，F，问是否存在直线l，使得向量

DF

+

BE

=

0

，若存在，指出这样的直线有多少条？若不存在，请说明理由．

查看答案和解析>>

科目：gzsx 来源： 题型：

在平面直角坐标系xOy中，已知圆心在x轴上、半径为2的圆C位于y轴右侧，且与直线x-

3

y+2=0相切．
（1）求圆C的方程；
（2）在圆C上，是否存在点M（m，n），使得直线l：mx+ny=1与圆O：x²+y²=1相交于不同的两点A，B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．

查看答案和解析>>

科目：gzsx 来源：2012-2013学年湖北省武汉市武昌区高三上学期期末调研测试理科数学试卷（解析版） 题型：解答题

（本题满分13分）

设点P是圆x² +y² =4上任意一点，由点P向x轴作垂线PP₀，垂足为P_o，且．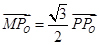

（Ⅰ）求点M的轨迹C的方程；

（Ⅱ）设直线：y=kx+m(m≠0)与（Ⅰ）中的轨迹C交于不同的两点A，B．

（1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；

（2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线过定点(Q点除外)，并求出该定点的坐标．

查看答案和解析>>

科目：gzsx 来源：2009年广东省广州市高考数学一模试卷（理科）（解析版） 题型：解答题

已知动圆C过点A（-2，0），且与圆M：（x-2）²+y²=64相内切
（1）求动圆C的圆心的轨迹方程；
（2）设直线l：y=kx+m（其中k，m∈Z）与（1）所求轨迹交于不同两点B，D，与双曲线

交于不同两点E，F，问是否存在直线l，使得向量

，若存在，指出这样的直线有多少条？若不存在，请说明理由．

查看答案和解析>>

科目：gzsx 来源： 题型：

已知动点M到点F(，0)的距离与到直线x=的距离之比为.

(Ⅰ)求动点M的轨迹C的方程；

(Ⅱ)若过点E(0，1)的直线与曲线C在y轴左侧交于不同的两点A、B，点P(-2，0)满足=，求直线PN在y轴上的截距d的取值范围.

查看答案和解析>>

科目：gzsx 来源：2013年高考数学压轴大题训练：解析几何中的探究性问题（解析版） 题型：解答题

已知动圆C过点A（-2，0），且与圆M：（x-2）²+y²=64相内切
（1）求动圆C的圆心的轨迹方程；
（2）设直线l：y=kx+m（其中k，m∈Z）与（1）所求轨迹交于不同两点B，D，与双曲线

交于不同两点E，F，问是否存在直线l，使得向量

，若存在，指出这样的直线有多少条？若不存在，请说明理由．

查看答案和解析>>

科目：gzsx 来源： 题型：

设点P是圆x² +y² =4上任意一点，由点P向x轴作垂线PP₀，垂足为P_o，且．

（Ⅰ）求点M的轨迹C的方程；

（Ⅱ）设直线：y=kx+m(m≠0)与（Ⅰ）中的轨迹C交于不同的两点A，B．

（1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；

（2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线过定点(Q点除外)，并求出该定点的坐标．

查看答案和解析>>

科目：gzsx 来源：2012-2013学年河南省信阳市商城高中高二（上）12月月考数学试卷（文科）（解析版） 题型：解答题

已知动圆C过点A（-2，0），且与圆M：（x-2）²+y²=64相内切
（1）求动圆C的圆心的轨迹方程；
（2）设直线l：y=kx+m（其中k，m∈Z）与（1）所求轨迹交于不同两点B，D，与双曲线

交于不同两点E，F，问是否存在直线l，使得向量

，若存在，指出这样的直线有多少条？若不存在，请说明理由．

查看答案和解析>>

科目：gzsx 来源：2011年四川省南充市高考数学一模试卷（理科）（解析版） 题型：解答题

已知动圆C过点A（-2，0），且与圆M：（x-2）²+y²=64相内切
（1）求动圆C的圆心的轨迹方程；
（2）设直线l：y=kx+m（其中k，m∈Z）与（1）所求轨迹交于不同两点B，D，与双曲线

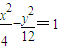交于不同两点E，F，问是否存在直线l，使得向量

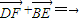，若存在，指出这样的直线有多少条？若不存在，请说明理由．

查看答案和解析>>

科目：gzsx 来源：2012年宁夏高考数学仿真模拟试卷10（文科）（解析版） 题型：解答题

已知动圆C过点A（-2，0），且与圆M：（x-2）²+y²=64相内切
（1）求动圆C的圆心的轨迹方程；
（2）设直线l：y=kx+m（其中k，m∈Z）与（1）所求轨迹交于不同两点B，D，与双曲线

交于不同两点E，F，问是否存在直线l，使得向量

，若存在，指出这样的直线有多少条？若不存在，请说明理由．

查看答案和解析>>

练习册

高中

初中

小学

若直线x+y+m=0（m＞0）与圆x^2+y^2=2交于不同的两点A、B，O是坐标原点答案解析