精英家教网 >
试题搜索列表 >为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,设x2-1=y,则y2=(x2-1)2,原方程化为y2-5y+4=0,解此方程,得y1=1,y2=4. 当y=1时,x2-l=l,x2=2,∴x=± 2 . 当y=4时,x2-l=4,x2=5,∴x=± 5 ∴原方程的解为x1=− 2 ,x2= 2 ,x3=− 5 ,x4= 5 . 以上方法就叫换元法,达到了降次的目的,体现了转化的思想.运用上述方法解下列方程: (1)x4-3x2-4=
为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,设x2-1=y,则y2=(x2-1)2,原方程化为y2-5y+4=0,解此方程,得y1=1,y2=4. 当y=1时,x2-l=l,x2=2,∴x=± 2 . 当y=4时,x2-l=4,x2=5,∴x=± 5 ∴原方程的解为x1=− 2 ,x2= 2 ,x3=− 5 ,x4= 5 . 以上方法就叫换元法,达到了降次的目的,体现了转化的思想.运用上述方法解下列方程: (1)x4-3x2-4=答案解析
科目:czsx
来源:
题型:阅读理解
阅读材料:为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1看作一个整体,然后设x
2-1=y…①,
那么原方程可化为y
2-5y+4=0,
解得y
1=1,y
2=4.
当y=1时,x
2-1=1,∴x
2=2,∴x=±
;
当y=4时,x
2-1=4,∴x
2=5,∴x=±
,
故原方程的解为x
1=
,x
2=
-,x
3=
,x
4=
-.
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用
法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解方程x
4-x
2-6=0.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读材料,解答问题:为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1视为一个整体,然后设x
2-1=y原方程可化为y
2-5y+4=0,解此方程得y
1=1,y
2=4.当y=1时,x
2-1=1,∴x=±
;当y=4时,x
2-1=4,∴x=±
,∴原方程的解为x
1=
,x
2=-
,x
3=
,x
4=-
.
(1)填空:在原方程得到方程y
2-5y+4=0的过程中,利用了
换元
换元
法达到了降次的目的,体现了
转化
转化
的数学思想
(2)解方程:(x
2-x)
2-8(x
2-x)+12=0.
查看答案和解析>>
科目:czsx
来源:
题型:
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可将x
2-1看作一个整体,然后设x
2-1=y;那么原方程可化为y
2-5y+4=0①,解这个方程,得y
1=1,y
2=4.当y
1=1时,x
2-1=1,所以
x=±;当y
2=4时,x
2-1=4,所以
x=±则原方程的解为
x1=,
x2=-,
x3=,
x4=-解答下列问题:
(1)填空:在由原方程得到方程①的过程中,利用
换元
换元
法达到降次的目的,体现了
转化
转化
的数学思想;
(2)请利用上述方法解方程:(x
2-2)
2-5(x
2-2)+6=0.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读下列材料:
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1看作一个整体,设x
2-1=y,则原方程可化为y
2-5y+4=0,解得y
1=1,y
2=4.
当y
1=1时,x
2-1=1,∴
x=±;当y
2=4时,x
2-1=4,∴
x=±.
因此原方程的解为:
x1=,x2=-,x3=,x4=-.
(1)已知方程
=x2-2x-3,如果设x
2-2x=y,那么原方程可化为
(写成关于y的一元二次方程的一般形式).
(2)根据阅读材料,解方程:x(x+3)(x
2+3x+2)=24.
查看答案和解析>>
科目:czsx
来源:
题型:
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1视为一个整体,然后设x
2-1=y,则
(x
2-1)2=y
2,原方程化为y
2-5y+4=0.①
解得y
1=1,y
2=4
当y=1时,x
2-1=1.∴x
2=2.∴x=±
;
当y=4时,x
2-1=4,∴x
2=5,∴x=±
.
∴原方程的解为x
1=
,x
2=-
,x
3=
,x
4=-
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用
换元
换元
法达到了降次的目的,体现了
转化
转化
的数学思想.
(2)解方程:x
4-x
2-6=0.
查看答案和解析>>
科目:czsx
来源:
题型:
材料:为解方程x
4-x
2-6=0,可将方程变形为(x
2)
2-x
2-6=0,
然后设x
2=y,则(x
2)
2=y
2,原方程化为y
2-y-6=0…①,
解得y
1=-2,y
2=3.当y
1=-2时,x
2=-2无意义,舍去;
当y
2=3时,x
2=3,解得x=±
.
所以原方程的解为x
1=
,x
2=-
.
问题:(1)在原方程得到方程①的过程中,利用
换元
换元
法达到了降次的目的,体现了
转化
转化
的数学思想;
(2)利用本题的解题方法,解方程(x
2-x)
2-4(x
2-x)-12=0.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读下面材料:解答问题
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将(x
2-1)看作一个整体,然后设x
2-1=y,那么原方程可化为y
2-5y+4=0,解得y
1=1,y
2=4.当y=1时,x
2-1=1,∴x
2=2,∴x=±
;当y=4时,x
2-1=4,∴x
2=5,∴x=±
,故原方程的解为x
1=
,x
2=-
,x
3=
,x
4=-
.
上述解题方法叫做换元法;请利用换元法解方程.(x
2-x)
2-4(x
2-x)-12=0.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读下面材料:
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1视为一个整体,然后设x
2-1=y,则(x
2-1)
2=y
2,原方程化为y
2-5y+4=0.①
解得y
1=1,y
2=4.
当y
1=1时,x
2-1=1,所以x
2=2,所以
x=±;
当y
2=4时,x
2-1=4,所以x
2=5,所以
x=±;
所以原方程的解为:
x1=,x2=-,x3=,x4=-.
(1)在由原方程得到方程①的过程中,利用
换元
换元
法达到了降次的目的,体现了
转化
转化
的数学思想;
(2)解方程:x
4-3x
2-4=0.
查看答案和解析>>
科目:czsx
来源:
题型:
阅读材料:为了解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1视为一个整体,然后设x
2-1=y,(x
2-1)
2=y
2,
则原方程可化为y
2-5y+4=0①
解得y
1=1,y
2=4.
当y=1时,x
2-1=1,x
2=2,∴x=±
当y=4时,x
2-1=4,x
2=5,∴x=±
∴原方程的解为:x
1=
,x2=-,x3=x4=-解答问题:仿造上题解方程:x
4-6x
2+8=0.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
请同学们认真阅读下面的一段文字材料,然后解答题目中提出的有关问题.
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1视为一个整体,然后设x
2-1=y,则原方程可化为y
2-5y+4=0①
解得y
1=1,y
2=4
当y=1时,x
2-1=1,∴x
2=2,x=±
当y=4时,x
2-1=4,∴x
2=5,x=±
∴原方程的解为x
1=
,x
2=-
,x
3=
,x
4=-
解方程:(1)(3x+5)
2-4(3x+5)+3=0
(2)x
4-10x
2+9=0.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读材料:为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1看作一个整体,
设x
2-1=y…①,
那么原方程可化为y
2-5y+4=0,解得y
1=1,y
2=4,
当y=1时,x
2-1=1,∴x
2=2,∴
x=±;
当y=4时,x
2-1=4,∴x
2=5,∴
x=±,
故原方程的解为
x1=,
x2=-,
x3=,
x4=-.
以上解题方法叫做换元法,在由原方程得到方程①的过程中,利用换元法达到了解方程的目的,体现了转化的数学思想;请利用以上知识解方程:
(1)x
4-x
2-6=0. (2)(x
2+x)
2+(x
2+x)=6.
查看答案和解析>>
科目:czsx
来源:
题型:
材料:为解方程x
4-x
2-6=0,可将方程变形为(x
2)
2-x
2-6=0,然后设x
2=y,则(x
2)
2=y
2,原方程化为y
2-y-6=0…①,
解得y
1=-2,y
2=3.
当y
1=-2时,x
2=-2无意义,舍去;当y
2=3时,x
2=3,解得x=±
.
所以原方程的解为x
1=
,x
2=-
.
问题:利用本题的解题方法,解方程(x
2-x)
2-4(x
2-x)-12=0.
查看答案和解析>>
科目:czsx
来源:2011-2012学年宁夏固原市西吉县回民中学九年级(上)期中数学试卷(解析版)
题型:解答题
阅读材料:为了解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1视为一个整体,然后设x
2-1=y,(x
2-1)
2=y
2,
则原方程可化为y
2-5y+4=0①
解得y
1=1,y
2=4.
当y=1时,x
2-1=1,x
2=2,∴x=±
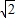
当y=4时,x
2-1=4,x
2=5,∴x=±
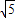
∴原方程的解为:x
1=
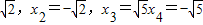
解答问题:仿造上题解方程:x
4-6x
2+8=0.
查看答案和解析>>
科目:czsx
来源:第1章《一元二次方程》常考题集(13):1.2 解一元二次方程的算法(解析版)
题型:解答题
阅读下面材料:解答问题
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将(x
2-1)看作一个整体,然后设x
2-1=y,那么原方程可化为y
2-5y+4=0,解得y
1=1,y
2=4.当y=1时,x
2-1=1,∴x
2=2,∴x=±
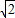
;当y=4时,x
2-1=4,∴x
2=5,∴x=±

,故原方程的解为x
1=

,x
2=-

,x
3=

,x
4=-

.
上述解题方法叫做换元法;请利用换元法解方程.(x
2-x)
2-4(x
2-x)-12=0.
查看答案和解析>>
科目:czsx
来源:2012-2013学年江苏省无锡市钱桥中学九年级(上)期中数学试卷(解析版)
题型:解答题
材料:为解方程x
4-x
2-6=0,可将方程变形为(x
2)
2-x
2-6=0,然后设x
2=y,则(x
2)
2=y
2,原方程化为y
2-y-6=0…①,解得y
1=-2,y
2=3.当y
1=-2时,x
2=-2无意义,舍去;当y
2=3时,x
2=3,解得x=±
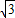
.所以原方程的解为x
1=

,x
2=-
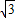
.
问题:(1)在原方程得到方程①的过程中,利用______法达到了降次的目的,体现了______ 的数学思想;
(2)利用本题的解题方法,解方程(x
2-x)
2-4(x
2-x)-12=0.
查看答案和解析>>
科目:czsx
来源:2009-2010学年江西省九年级(上)期末数学试卷1(解析版)
题型:解答题
阅读下面材料:解答问题
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将(x
2-1)看作一个整体,然后设x
2-1=y,那么原方程可化为y
2-5y+4=0,解得y
1=1,y
2=4.当y=1时,x
2-1=1,∴x
2=2,∴x=±

;当y=4时,x
2-1=4,∴x
2=5,∴x=±

,故原方程的解为x
1=

,x
2=-

,x
3=

,x
4=-

.
上述解题方法叫做换元法;请利用换元法解方程.(x
2-x)
2-4(x
2-x)-12=0.
查看答案和解析>>
科目:czsx
来源:第23章《一元二次方程》常考题集(20):23.3 实践与探索(解析版)
题型:解答题
阅读材料:为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1看作一个整体,然后设x
2-1=y…①,
那么原方程可化为y
2-5y+4=0,
解得y
1=1,y
2=4.
当y=1时,x
2-1=1,∴x
2=2,∴x=±

;
当y=4时,x
2-1=4,∴x
2=5,∴x=±

,
故原方程的解为x
1=

,x
2=

,x
3=

,x
4=

.
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用______法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解方程x
4-x
2-6=0.
查看答案和解析>>
科目:czsx
来源:第2章《一元二次方程》常考题集(21):2.5 为什么是0.168(解析版)
题型:解答题
阅读材料:为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将x
2-1看作一个整体,然后设x
2-1=y…①,
那么原方程可化为y
2-5y+4=0,
解得y
1=1,y
2=4.
当y=1时,x
2-1=1,∴x
2=2,∴x=±

;
当y=4时,x
2-1=4,∴x
2=5,∴x=±

,
故原方程的解为x
1=

,x
2=

,x
3=

,x
4=

.
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用______法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解方程x
4-x
2-6=0.
查看答案和解析>>
科目:czsx
来源:第22章《一元二次方程》常考题集(13):22.2 降次——解一元二次方程(解析版)
题型:解答题
阅读下面材料:解答问题
为解方程(x
2-1)
2-5(x
2-1)+4=0,我们可以将(x
2-1)看作一个整体,然后设x
2-1=y,那么原方程可化为y
2-5y+4=0,解得y
1=1,y
2=4.当y=1时,x
2-1=1,∴x
2=2,∴x=±

;当y=4时,x
2-1=4,∴x
2=5,∴x=±

,故原方程的解为x
1=

,x
2=-

,x
3=

,x
4=-

.
上述解题方法叫做换元法;请利用换元法解方程.(x
2-x)
2-4(x
2-x)-12=0.
查看答案和解析>>

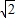
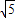
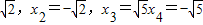
 ;
; ,
, ,x2=
,x2=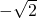 ,x3=
,x3= ,x4=
,x4=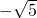 .
.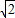 ;当y=4时,x2-1=4,∴x2=5,∴x=±
;当y=4时,x2-1=4,∴x2=5,∴x=± ,故原方程的解为x1=
,故原方程的解为x1= ,x2=-
,x2=- ,x3=
,x3= ,x4=-
,x4=- .
.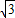 .所以原方程的解为x1=
.所以原方程的解为x1= ,x2=-
,x2=-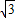 .
. ;当y=4时,x2-1=4,∴x2=5,∴x=±
;当y=4时,x2-1=4,∴x2=5,∴x=± ,故原方程的解为x1=
,故原方程的解为x1= ,x2=-
,x2=- ,x3=
,x3= ,x4=-
,x4=- .
. ;
; ,
, ,x2=
,x2= ,x3=
,x3= ,x4=
,x4= .
. ;
; ,
, ,x2=
,x2= ,x3=
,x3= ,x4=
,x4= .
. ;当y=4时,x2-1=4,∴x2=5,∴x=±
;当y=4时,x2-1=4,∴x2=5,∴x=± ,故原方程的解为x1=
,故原方程的解为x1= ,x2=-
,x2=- ,x3=
,x3= ,x4=-
,x4=- .
.