
科目:gzsx 来源: 题型:
| 3 |
| ||
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 8 |
| ||
| 3 |
| MP |
| PN |
| AP |
| MN |
科目:gzsx 来源:2014届山东济宁泗水一中高二12月质量检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知焦点在 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线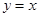 对称.
对称.
(1)求双曲线C的方程;
(2)设直线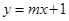 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线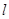 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线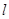 在
在 轴上的截距b的取值范围.
轴上的截距b的取值范围.
科目:gzsx 来源: 题型:
已知焦点在![]() 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线![]() 对称.
对称.
(1)求双曲线C的方程;
(2)设直线![]() 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线![]() 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线![]() 在
在![]() 轴上的截距b的取值范围.(12分)
轴上的截距b的取值范围.(12分)
科目:gzsx 来源:浙江省杭州学军中学09-10学年高二上学期期中考试(理) 题型:解答题
已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点A(0, )为圆心、1为半径的圆相切,又知双曲线C的一个焦点与点A关于直线
)为圆心、1为半径的圆相切,又知双曲线C的一个焦点与点A关于直线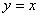 对称.
对称.
(1)求双曲线C的方程;
(2)求与双曲线C共渐近线,且过点 的双曲线方程,并求出此双曲线方程的焦点坐标,长轴长和虚轴长.
的双曲线方程,并求出此双曲线方程的焦点坐标,长轴长和虚轴长.
科目:gzsx 来源:重庆市高考真题 题型:解答题
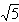 ,0)为右焦点的双曲线C的离心率,
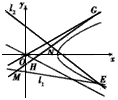
,0)为右焦点的双曲线C的离心率,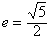 。
。
科目:gzsx 来源: 题型:
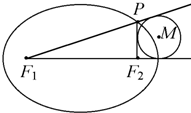 (2007•浦东新区二模)如图,已知点P在焦点为F1、F2的椭圆上运动,则与△PF1F2的边PF2相切,且与边F1F2,F1P的延长线相切的圆的圆心M一定在( )
(2007•浦东新区二模)如图,已知点P在焦点为F1、F2的椭圆上运动,则与△PF1F2的边PF2相切,且与边F1F2,F1P的延长线相切的圆的圆心M一定在( )科目:gzsx 来源: 题型:
 (2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率e=
(2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率e=
| ||
| 2 |
科目:gzsx 来源: 题型:
已知抛物线![]() (
(![]() )焦点为
)焦点为![]() ,其准线与
,其准线与![]() 轴交于点
轴交于点![]() ,以
,以![]() 、
、![]() 为焦点,离心率为
为焦点,离心率为![]() 的椭圆
的椭圆![]() 与抛物线
与抛物线![]() 在
在![]() 轴上方的一个交点为
轴上方的一个交点为![]() .
.
(1)当![]() 时,求椭圆的标准方程及其右准线的方程;
时,求椭圆的标准方程及其右准线的方程;
(2)用![]() 表示P点的坐标;
表示P点的坐标;
(3)是否存在实数![]() ,使得
,使得![]() 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
科目:gzsx 来源: 题型:
在平面直角坐标系![]() ,已知圆心在第二象限、半径为
,已知圆心在第二象限、半径为![]() 的圆C与直线y=x相切于
的圆C与直线y=x相切于
坐标原点O.椭圆![]() 与圆C的一个交点到椭圆两焦点的距离之和为
与圆C的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆C的方程;
(2)圆C上是否存在异于原点的点Q,使![]() (F为椭圆右焦点),若存在,请
(F为椭圆右焦点),若存在,请
求出点Q的坐标;若不存在,请说明理由.
科目:gzsx 来源:2013届度吉林省吉林市高二上学期期末理科数学试卷 题型:解答题
已知抛物线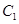 :
: ,焦点为
,焦点为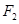 ,其准线与
,其准线与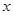 轴交于点
轴交于点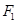 ;椭圆
;椭圆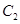 :分别以
:分别以 为左、右焦点,其离心率
为左、右焦点,其离心率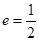 ;且抛物线
;且抛物线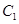 和椭圆
和椭圆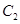 的一个交点记为
的一个交点记为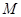 .
.
(1)当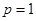 时,求椭圆
时,求椭圆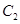 的标准方程;
的标准方程;
(2)在(1)的条件下,若直线 经过椭圆
经过椭圆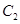 的右焦点
的右焦点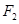 ,且与抛物线
,且与抛物线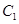 相交于
相交于 两点,若弦长
两点,若弦长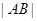 等于
等于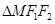 的周长,求直线
的周长,求直线 的方程.
的方程.
科目:gzsx 来源: 题型:
在平面直角坐标系![]() 中,已知圆心在直线
中,已知圆心在直线![]() 上,半径为
上,半径为![]() 的圆C经过坐标原点O,椭圆
的圆C经过坐标原点O,椭圆![]() 与圆C的一个交点到椭圆两焦点的距离之和为10.
与圆C的一个交点到椭圆两焦点的距离之和为10.
(1)求圆C的方程;
(2)若F为椭圆的右焦点,点P在圆C上,且满足![]() ,求点P
,求点P
科目:gzsx 来源:2010-2011学年湖南省高二上学期质量检测数学理卷 题型:解答题
(本小题满分12分)已知抛物线 :
: ,焦点为
,焦点为 ,其准线与
,其准线与 轴交于点
轴交于点 ;椭圆
;椭圆 :分别以
:分别以 为左、右焦点,其离心率
为左、右焦点,其离心率 ;且抛物线
;且抛物线 和椭圆
和椭圆 的一个交点记为
的一个交点记为 .
.
(1)当 时,求椭圆
时,求椭圆 的标准方程;
的标准方程;
(2)在(1)的条件下,若直线 经过椭圆
经过椭圆 的右焦点
的右焦点 ,且与抛物线
,且与抛物线 相交于
相交于 两点,若弦长
两点,若弦长 等于
等于 的周长,求直线
的周长,求直线 的方程.
的方程.
科目:gzsx 来源:2010年山东省高考数学押题试卷(理科)(解析版) 题型:解答题
 .
.科目:gzsx 来源:2007-2008学年浙江省宁波市柔石中学高三(上)月考数学试卷3(解析版) 题型:解答题
 的焦点,离心率等于
的焦点,离心率等于 .
. ,
, ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.科目:gzsx 来源:2007年山东省威海市高考数学一模试卷(理科)(解析版) 题型:解答题
 的焦点,离心率等于
的焦点,离心率等于 .
. ,
, ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.科目:gzsx 来源:2009-2010学年江西省吉安市白鹭洲中学高二(下)5月月考数学试卷(文科)(解析版) 题型:解答题
 的焦点,离心率等于
的焦点,离心率等于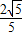 .
.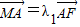 ,
, ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.科目:gzsx 来源:2010年山东省高考数学押题卷(理科)(解析版) 题型:解答题
 .
.