
科目:gzsx 来源: 题型:
. (本小题满分14分)
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
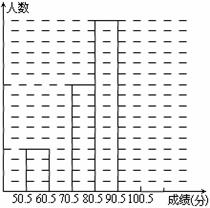
(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频数条形图;
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
科目:gzsx 来源:2014届海南琼海嘉积中学高二上教学监测(三)文科数学试卷(解析版) 题型:解答题
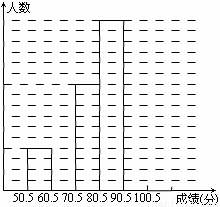
(本小题满分12分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
|
分组 |
频数 |
频率 |
|
50.5~60.5 |
6 |
0.08 |
|
60.5~70.5 |
|
0.16 |
|
70.5~80.5 |
15 |
|
|
80.5~90.5 |
24 |
0.32 |
|
90.5~100.5 |
|
|
|
合计 |
75 |
|
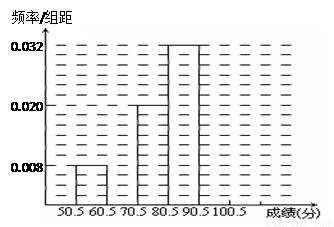
(Ⅰ)填充频率分布表的空格(将答案直接填在答题卡的表格内);
(Ⅱ)补全频率分布直方图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
科目:gzsx 来源: 题型:
(本小题满分12分)
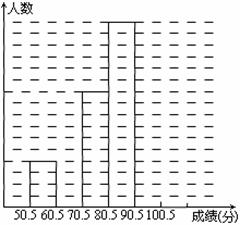
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有1000名学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
(1)求频率分布表中的![]() ,
,![]() 值,并补全频数条形图;
值,并补全频数条形图;
(2)根据频数条形图估计该样本的中位数是多少?
(3)若成绩在65.5~85.5分的学生为三等奖,问该校获得三等奖的学生约为多少人?
| 频率分布表 | ||
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 |
| 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | |
| 90.5~100.5 |
| |
| 合计 | 1 | |
科目:gzsx 来源: 题型:
(本小题满分10分) 为了让学生了解更多“社会法律”知识,某中学举行了一次“社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 | 频数 | 频率 |
| 60.5~70.5 | 1 | 0.16 |
| 70.5~80.5 | 10 | 2 |
| 80.5~90.5 | 18 | 0.36 |
| 90.5~100.5 | 3 | 4 |
| 合计 | 50 | 1 |
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号 ;(2)填充频率分布表的空格1 2 3 4 并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少人
科目:gzsx 来源:2011年吉林省高二上学期期末质量检测数学文卷 题型:解答题
(本小题满分12分)
为了让学生更多地了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有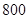 名学生参加了这次竞赛。为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为
名学生参加了这次竞赛。为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为 分)进行统计。请你根据下面的频率分布表,解答下列问题:
分)进行统计。请你根据下面的频率分布表,解答下列问题:
|
序号 ( |
分组 (分数) |
本组中间值
|
频数 (人数) |
频率
|
|
|
|
|
①[] |
|
|
|
|
|
|
②] |
|
|
|
|
③ |
|
|
|
|
|
④ |
⑤ |
|
合 计 |
|
|
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于 分的同学能获奖,请估计在参赛的
分的同学能获奖,请估计在参赛的 名学生中大概有多少同学获奖?
名学生中大概有多少同学获奖?
|
科目:gzsx 来源:2010年广东省高二上学期10月月考理科数学卷 题型:解答题
(本题满分14分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数条形图,解答下列问题:
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,问该校获得二等奖的学生约为多少人?
|
分组 |
频数 |
频率 |
|
50.5~60.5 |
4 |
0.08 |
|
60.5~70.5 |
|
0.16 |
|
70.5~80.5 |
10 |
|
|
80.5~90.5 |
16 |
0.32 |
|
90.5~100.5 |
|
|
|
合计 |
50 |
|
科目:gzsx 来源:2011-2012学年山东省高三9月月考理科数学 题型:解答题
(本小题满分14分)设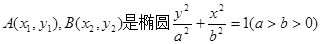 上的两点,已知向量
上的两点,已知向量 ,
, ,若
,若 且椭圆的离心率
且椭圆的离心率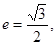 短轴长为2,
短轴长为2, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线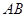 过椭圆的焦点
过椭圆的焦点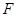 (0,c),(c为半焦距),求直线
(0,c),(c为半焦距),求直线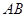 的斜率
的斜率 的值;
的值;
(Ⅲ)试问: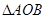 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
科目:gzsx 来源: 题型:
(本小题满分14分)
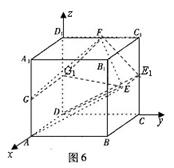
如图6,已知正方体![]() 的棱长为2,点
的棱长为2,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 、
、![]() 分别是棱
分别是棱![]() 的中点.设点
的中点.设点![]() 分别是点
分别是点![]() ,
,![]() 在平面
在平面![]() 内的正投影.
内的正投影.
(1)求以![]() 为顶点,以四边形
为顶点,以四边形![]() 在平面
在平面![]() 内的正投影为底面边界的棱锥的体积;
内的正投影为底面边界的棱锥的体积;
(2)证明:直线![]() 平面
平面![]() ;
;
(3)求异面直线![]() 所成角的正弦值.
所成角的正弦值.
科目:gzsx 来源:2012-2013学年湖北武汉部分重点中学高二上期中考试理数学试卷(带解析) 题型:解答题
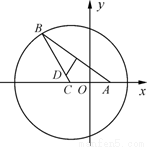
(本小题满分14分)如图所示,已知以点 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线 与圆
与圆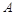 相交于
相交于 ,
,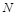 两点,
两点, 是
是 的中点,直线
的中点,直线 与
与 相交于点
相交于点 .
.
(1)求圆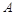 的方程;
的方程;
(2)当 时,求直线
时,求直线 的方程.
的方程.
(3) 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
科目:gzsx 来源:2011-2012学年广东省深圳市高三第一次调研理科数学 题型:解答题
(本小题满分14分)
如图7,已知椭圆 :
: 的离心率为
的离心率为 ,以椭圆
,以椭圆 的左顶点
的左顶点 为
为
圆心作圆 :
: ,设圆
,设圆 与椭圆
与椭圆 交于点
交于点 与点
与点 .
.
(1)求椭圆 的方程;
的方程;
(2)求 的最小值,并求此时圆
的最小值,并求此时圆 的方程;
的方程;
(3)设点 是椭圆
是椭圆 上异于
上异于 的任意一点,且直线
的任意一点,且直线 分别与
分别与 轴交于点
轴交于点
 ,
, 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.
科目:gzsx 来源:2010-2011学年广东省高三综合测试数学文卷 题型:解答题
(本小题满分14分)
为了进一步实现节能,在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外
墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热
层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)。与隔热层
厚度x(单位:cm)满足关系:
 ,若不建隔热层,每年能源消耗费用为8万元;设f(x)为
,若不建隔热层,每年能源消耗费用为8万元;设f(x)为
隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
科目:gzsx 来源:2011-2012年广东省广州市高二上学期期中考试理科数学 题型:解答题
(本小题满分14分)
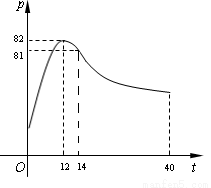
某校学生社团心理学研究小组在对学生在一节课中上课注意力集中情况的调查研究中,发现其注意力指数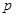 与听课时间
与听课时间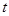 之间的关系满足如图所示的曲线.当
之间的关系满足如图所示的曲线.当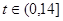 时,曲线是二次函数图象的一部分,
时,曲线是二次函数图象的一部分,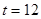 为其对称轴;当
为其对称轴;当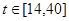 时,曲线是函数
时,曲线是函数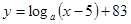 (
(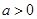 且
且 )图象的一部分.根据专家研究,当注意力指数
)图象的一部分.根据专家研究,当注意力指数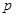 大于80时听课效果最佳.
大于80时听课效果最佳.
(1) 试求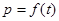 的函数关系式;
的函数关系式;
(2) 老师在什么时段内安排重点内容能使得学生听课效果最佳?
请说明理由.
科目:gzsx 来源:2014届湖北武汉部分重点中学高二上期中考试理数学试卷(解析版) 题型:解答题
(本小题满分14分)如图所示,已知以点 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线 与圆
与圆 相交于
相交于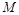 ,
, 两点,
两点, 是
是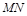 的中点,直线
的中点,直线 与
与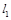 相交于点
相交于点 .
.

(1)求圆 的方程;
的方程;
(2)当 时,求直线
时,求直线 的方程.
的方程.
(3) 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
科目:gzsx 来源:2012届山东省曲阜师大附中高三9月月考理科数学 题型:解答题
(本小题满分14分)设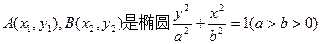 上的两点,已知向量
上的两点,已知向量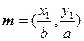 ,
,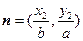 ,若
,若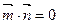 且椭圆的离心率
且椭圆的离心率 短轴长为2,
短轴长为2,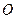 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线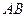 过椭圆的焦点
过椭圆的焦点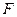 (0,c),(c为半焦距),求直线
(0,c),(c为半焦距),求直线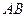 的斜率
的斜率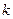 的值;
的值;
(Ⅲ)试问: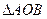 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
科目:gzsx 来源: 题型:
(2009广东卷理)(本小题满分14分)
如图6,已知正方体![]() 的棱长为2,点
的棱长为2,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 、
、![]() 分别是棱
分别是棱![]() 的中点.设点
的中点.设点![]() 分别是点
分别是点![]() ,
,![]() 在平面
在平面![]() 内的正投影.
内的正投影.
(1)求以![]() 为顶点,以四边形
为顶点,以四边形![]() 在平面
在平面![]() 内的正投影为底面边界的棱锥的体积;
内的正投影为底面边界的棱锥的体积;
(2)证明:直线![]() 平面
平面![]() ;
;
(3)求异面直线![]() 所成角的正弦值.
所成角的正弦值.

科目:gzsx 来源:2010-2011学年江西省高三联合考试数学文卷 题型:解答题
(本小题满分14分)
如图,在 ,已知A(-
,已知A(- ,0),
B(
,0),
B( ,0),
CD
,0),
CD AB于D,
AB于D,  的垂心为H,且
的垂心为H,且
(Ⅰ)求点H的轨迹方程;

(Ⅱ)若过定点F(0,2)的直线交曲线 于不同的两点
于不同的两点 (点
(点 在F,H之间),且满足
在F,H之间),且满足 ,求
,求 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
(本小题满分14分)
如图6,已知正方体![]() 的棱长为2,点
的棱长为2,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 、
、![]() 分别是棱
分别是棱![]() 的中点.设点
的中点.设点![]() 分别是点
分别是点![]() ,
,![]() 在平面
在平面![]() 内的正投影.
内的正投影.
(1)求以![]() 为顶点,以四边形
为顶点,以四边形![]() 在平面
在平面![]() 内的正投影为底面边界的棱锥的体积;
内的正投影为底面边界的棱锥的体积;
(2)证明:直线![]() 平面
平面![]() ;
;
(3)求异面直线![]() 所成角的正弦值.
所成角的正弦值.
科目:gzsx 来源:2011-2012学年四川省资阳市二下学期期末质量检测理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
如图所示,已知圆 ,
,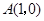 为定点,
为定点, 为圆
为圆 上的动点,线段
上的动点,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,点
,点 的轨迹为曲线E.
的轨迹为曲线E.
(Ⅰ)求曲线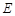 的方程;
的方程;
(Ⅱ)过点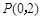 作直线
作直线 交曲线
交曲线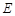 于
于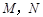 两点,设线段
两点,设线段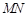 的中垂线交
的中垂线交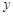 轴于点
轴于点 ,求实数m的取值范围.
,求实数m的取值范围.
科目:gzsx 来源: 题型:
(2009广东卷理)(本小题满分14分)
 如图6,已知正方体
如图6,已知正方体![]() 的棱长为2,点
的棱长为2,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 、
、![]() 分别是棱
分别是棱![]() 的中点.设点
的中点.设点![]() 分别是点
分别是点![]() ,
,![]() 在平面
在平面![]() 内的正投影.
内的正投影.
(1)求以![]() 为顶点,以四边形
为顶点,以四边形![]() 在平面
在平面![]() 内的正投影为底面边界的棱锥的体积;
内的正投影为底面边界的棱锥的体积;
(2)证明:直线![]() 平面
平面![]() ;
;
(3)求异面直线![]() 所成角的正弦值.
所成角的正弦值.
科目:gzsx 来源: 题型:
(本小题满分14分)
 如图6,已知圆
如图6,已知圆![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() 及上顶点
及上顶点![]() ,过椭圆外一点
,过椭圆外一点![]()
![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的方程;
(2)若![]() 求
求![]() 的取值范围.
的取值范围.