如图,RT△ABC中, AD⊥BC于D,tanB=cos∠DAC答案解析
科目:czsx
来源:
题型:
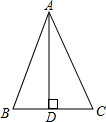
如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.请完成下面的说理过程.
解:∵AD⊥BC(已知)
∴∠ADB=
=Rt∠(垂直的意义)
在△ABD和△ACD中:
∴△ABD≌△ACD(
)
∴∠B=∠C(
)
查看答案和解析>>
科目:czsx
来源:
题型:
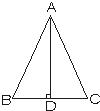
12、如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.
请完成下面的说理过程.
解:∵AD⊥BC(已知)
∴∠ADB=
∠ADC
=Rt∠(垂线的意义)
当把图形沿AD对折时,射线DB与DC
重合
∵BD=CD (
已知
)
∴点B与点
C
重合
∴△ABD与△ACD
重合
∴∠B=∠C (
重合角
)
查看答案和解析>>
科目:czsx
来源:浙江省期中题
题型:解答题
如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.请完成下面的说理过程.
解:∵AD⊥BC(已知)
∴∠ADB=
_________ =Rt∠(垂直的意义)
在△ABD和△ACD中:
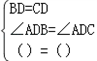
∴△ABD≌△ACD(
_________)
∴∠B=∠C(
_________)
查看答案和解析>>
科目:czsx
来源:
题型:填空题
如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.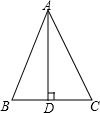
请完成下面的说理过程.
解:∵AD⊥BC(已知)
∴∠ADB=________=Rt∠(垂线的意义)
当把图形沿AD对折时,射线DB与DC________
∵BD=CD (________)
∴点B与点________重合
∴△ABD与△ACD________
∴∠B=∠C (________)
查看答案和解析>>
科目:czsx
来源:
题型:填空题
 如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.请完成下面的说理过程.
如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.请完成下面的说理过程.
解:∵AD⊥BC(已知)
∴∠ADB=________=Rt∠(垂直的意义)
在△ABD和△ACD中:
∴△ABD≌△ACD(________)
∴∠B=∠C(________)
查看答案和解析>>
科目:czsx
来源:
题型:
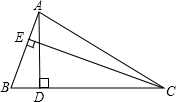
已知:如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,BE=2AE,且
AD=2,
sin∠BCE=,求CE的长.
查看答案和解析>>
科目:czsx
来源:
题型:

14、如图,在△ABC中,AD⊥BC于D.请你再添加一个条件,就可以确定△ABC是等腰三角形.你添加的条件是
BD=CD
.
查看答案和解析>>
科目:czsx
来源:
题型:
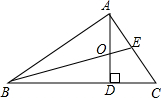
如图,在△ABC中,AD⊥BC于点D,BE平分∠ABC,∠ABC=40°,∠C=60°.求∠AOB,∠DAC的度数.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,那么∠ACB与∠DFE 的关系是( )
查看答案和解析>>
科目:czsx
来源:
题型:
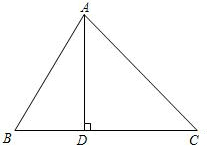
如图,在△ABC中,AD⊥BC于D,∠BAD=30°,∠ACD=45°,AB=5,求AC的长.
查看答案和解析>>
科目:czsx
来源:
题型:
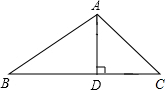
(2013•绥化)如图,在△ABC中,AD⊥BC于点D,AB=8,∠ABD=30°,∠CAD=45°,求BC的长.
查看答案和解析>>
科目:czsx
来源:
题型:
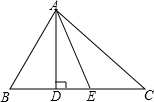
如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠AEC的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
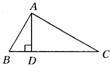
7、如图,在△ABC中,AD⊥BC于D,∠ABC=2∠C,求证:AC
2=AB
2+AB•BC.
查看答案和解析>>
科目:czsx
来源:
题型:
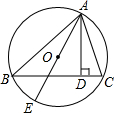
如图,在△ABC中,AD⊥BC于D,以AE为直径画圆,经过点B、C,求证:
(1)∠BAE=∠CAD;
(2)试说明:以等腰三角形的一腰为直径的圆平分底边.
查看答案和解析>>
科目:czsx
来源:
题型:
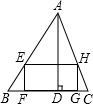
已知:如图,在△ABC中,AD⊥BC于D,BC=24,AD=18,矩形EFGH内接于△ABC,且EH=2EF,求矩形EFGH的周长.
查看答案和解析>>
科目:czsx
来源:
题型:
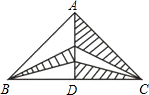
如图,在△ABC中,AD⊥BC于点D,DB=DC,若BC=6,AD=5,则图中阴影部分的面积为( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为
.
查看答案和解析>>
科目:czsx
来源:
题型:

8、如图,在△ABC中,AD⊥BC于D,再添加一个条件
AB=AC(符合要求即可)
,就可确定△ABD≌△ACD.
查看答案和解析>>
科目:czsx
来源:
题型:

25、已知如图:在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE相交于H,且BH=AC,连接CH并延长交AB于F,指出图中所有度数为45°的角,并任选一个来证明.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,AD⊥BC于点D,BE=ED=DC,∠1=∠2,则:
①AD是△ABC的边
BC
BC
上的高,也是
△ABD
△ABD
的边BD上的高,还是△ABE的边
BE
BE
上的高;
②AD既是
△AEC
△AEC
的边
EC
EC
上的中线,又是边
EC
EC
上的高,还是
∠EAC
∠EAC
的角平分线.
查看答案和解析>>

 如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.请完成下面的说理过程.
如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.请完成下面的说理过程. 12、如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.
12、如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.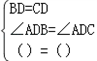
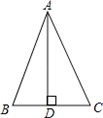

 如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.请完成下面的说理过程.
如图,在△ABC中,AD⊥BC于D,BD=CD,则∠B=∠C.请完成下面的说理过程.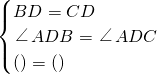
 如图,在△ABC中,AD⊥BC于D,以AE为直径画圆,经过点B、C,求证:
如图,在△ABC中,AD⊥BC于D,以AE为直径画圆,经过点B、C,求证: 25、已知如图:在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE相交于H,且BH=AC,连接CH并延长交AB于F,指出图中所有度数为45°的角,并任选一个来证明.
25、已知如图:在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE相交于H,且BH=AC,连接CH并延长交AB于F,指出图中所有度数为45°的角,并任选一个来证明. 如图,在△ABC中,AD⊥BC于点D,BE=ED=DC,∠1=∠2,则:
如图,在△ABC中,AD⊥BC于点D,BE=ED=DC,∠1=∠2,则: