
科目:czsx 来源: 题型:
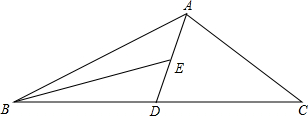 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线,科目:czsx 来源: 题型:
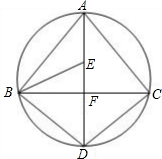 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.科目:czsx 来源: 题型:
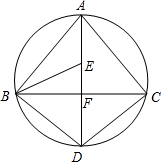 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,连接BD,CD.科目:czsx 来源: 题型:
 19、如图,AD为边BC边上中线,E为AD的中点,连BE交AC于F,则AF:AC=
19、如图,AD为边BC边上中线,E为AD的中点,连BE交AC于F,则AF:AC=科目:czsx 来源: 题型:
 24、如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.
24、如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.科目:czsx 来源: 题型:
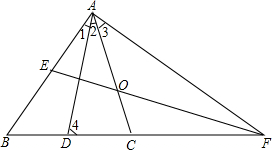 如图,AD为△ABC的角平分线,AD的中垂线交AB于点E、BC的延长线于点F,AC于EF交于点O.
如图,AD为△ABC的角平分线,AD的中垂线交AB于点E、BC的延长线于点F,AC于EF交于点O.科目:czsx 来源: 题型:
 我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连结AE.
我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连结AE.科目:czsx 来源: 题型:
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.科目:czsx 来源: 题型:
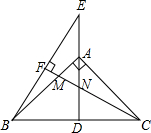 如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.| 5 |
| 4 |
| 15 |
| 8 |
| 9 |
| 8 |
科目:czsx 来源: 题型:
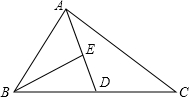 如图,AD为△ABC的中线,BE为△ABD的中线,
如图,AD为△ABC的中线,BE为△ABD的中线,科目:czsx 来源: 题型:
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.科目:czsx 来源: 题型:阅读理解
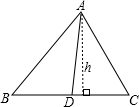 认真阅读,并回答下面问题:
认真阅读,并回答下面问题:| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源: 题型:
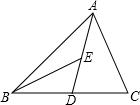
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.科目:czsx 来源: 题型:
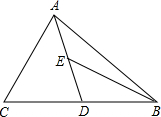
 如图,AD为△ABC的中线,BE为三角形ABD中线.
如图,AD为△ABC的中线,BE为三角形ABD中线.