精英家教网 >
试题搜索列表 >在△ABC中,AE:EB=1:2,EF‖BC,AD‖BC,交CE的延长线于D,试求S△AEF比去S△BCE的值
在△ABC中,AE:EB=1:2,EF‖BC,AD‖BC,交CE的延长线于D,试求S△AEF比去S△BCE的值答案解析
科目:czsx
来源:
题型:
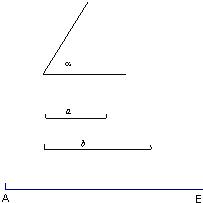
22、尺规作图,不写作法,保留作图痕迹:
如图,已知∠α和线段a,b.
(1)作△ABC,使得∠A=∠α,AB=a,AC=b,并且AC在给定的射线AE上;
(2)在△ABC中,作∠A的平分线AD,交BC于D.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 尺规作图,不写作法,保留作图痕迹:
尺规作图,不写作法,保留作图痕迹:
如图,已知∠α和线段a,b.
(1)作△ABC,使得∠A=∠α,AB=a,AC=b,并且AC在给定的射线AE上;
(2)在△ABC中,作∠A的平分线AD,交BC于D.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
尺规作图,不写作法,保留作图痕迹:
如图,已知∠α和线段a,b.
(1)作△ABC,使得∠A=∠α,AB=a,AC=b,并且AC在给定的射线AE上;
(2)在△ABC中,作∠A的平分线AD,交BC于D.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•凤阳县模拟)如图,在△ABC中,∠ACB=90°,AC=BC=2.E、F分别是射线AC、CB上的动点,且AE=BF,EF与AB交于点G,EH⊥AB于点H,设AE=x,GH=y,下面能够反映y与x之间函数关系的图象是( )
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•昆都仑区一模)如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
①△DEF是等腰直角三角形
②四边形CEDF不可能为正方形
③四边形CEDF的面积随点E位置的改变而发生变化
④点C到线段EF的最大距离为
其中正确的有
①④
①④
(填上你认为正确结论的所有序号)
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠BAC=90°,AC=BC,CD⊥AB,垂足为D,E是AC上一点,F为BC上一点,且AE=CF,连结DE,DF,若EF=10,求△DFE的面积.
查看答案和解析>>
科目:czsx
来源:
题型:

(2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为
.
其中正确结论的个数是( )
查看答案和解析>>
科目:czsx
来源:
题型:

已知:如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE和BF,且E,F为垂足.
(1)求证:EF=AE+BF;
(2)取AB的中点M,连接ME,MF.试判断△MEF的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
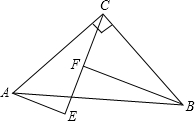
已知:如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
(1)求证:CF=AE;
(2)试判断线段EF、AE、BF之间的关系.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l的垂线AE、BF,E、F为垂足.

(1)当直线l不与底边AB相交时,求证:EF=AE+BF.
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB交于点D,请你探究直线l在如下三种可能的位置时,EF、AE、BF三者之间的数量关系.(直接填空)
①当AD>BD时,关系是:
AE=BF+EF
AE=BF+EF
.
②当AD=BD时,关系是:
AE=BF
AE=BF
.
③当AD<BD时,关系是:
BF=AE+EF
BF=AE+EF
.
查看答案和解析>>
科目:czsx
来源:
题型:
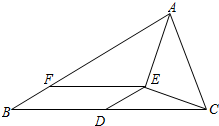
如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
查看答案和解析>>
科目:czsx
来源:2012-2013学年湖北省天门市十一校九年级4月联考数学试卷(解析版)
题型:选择题
在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:

①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:czsx
来源:2013届湖北省天门市十一校九年级4月联考数学试卷(带解析)
题型:单选题
在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:

①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:czsx
来源:2011年广东省八年级第二次月考数学卷
题型:解答题
如图:在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥GD于E,BF⊥CD交CD的延长线于F。求证:AE=EF+BF。

查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
查看答案和解析>>
科目:czsx
来源:北京期中题
题型:证明题
已知:如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
(1)求证:CF=AE;
(2)试判断线段EF、AE、BF之间的关系。
查看答案和解析>>
科目:czsx
来源:乐山
题型:单选题
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为
.
其中正确结论的个数是( )
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图1,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l的垂线AE、BF,E、F为垂足.
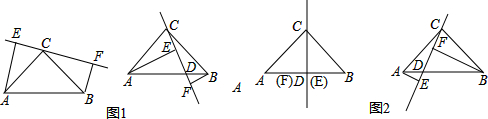
(1)当直线l不与底边AB相交时,求证:EF=AE+BF.
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB交于点D,请你探究直线l在如下三种可能的位置时,EF、AE、BF三者之间的数量关系.(直接填空)
①当AD>BD时,关系是:______.
②当AD=BD时,关系是:______.
③当AD<BD时,关系是:______.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
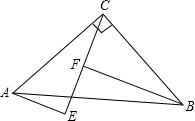 已知:如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
(1)求证:CF=AE;
(2)试判断线段EF、AE、BF之间的关系.
查看答案和解析>>
科目:czsx
来源:北京同步题
题型:证明题
如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=EF,AE=CE,AB与CF有什么位置关系?证明你的结论。
查看答案和解析>>

 22、尺规作图,不写作法,保留作图痕迹:
22、尺规作图,不写作法,保留作图痕迹: 尺规作图,不写作法,保留作图痕迹:
尺规作图,不写作法,保留作图痕迹: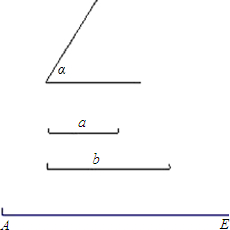
 (2013•凤阳县模拟)如图,在△ABC中,∠ACB=90°,AC=BC=2.E、F分别是射线AC、CB上的动点,且AE=BF,EF与AB交于点G,EH⊥AB于点H,设AE=x,GH=y,下面能够反映y与x之间函数关系的图象是( )
(2013•凤阳县模拟)如图,在△ABC中,∠ACB=90°,AC=BC=2.E、F分别是射线AC、CB上的动点,且AE=BF,EF与AB交于点G,EH⊥AB于点H,设AE=x,GH=y,下面能够反映y与x之间函数关系的图象是( ) (2013•昆都仑区一模)如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
(2013•昆都仑区一模)如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论: 如图,在△ABC中,∠BAC=90°,AC=BC,CD⊥AB,垂足为D,E是AC上一点,F为BC上一点,且AE=CF,连结DE,DF,若EF=10,求△DFE的面积.
如图,在△ABC中,∠BAC=90°,AC=BC,CD⊥AB,垂足为D,E是AC上一点,F为BC上一点,且AE=CF,连结DE,DF,若EF=10,求△DFE的面积. (2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
(2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论: 已知:如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE和BF,且E,F为垂足.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE和BF,且E,F为垂足. 已知:如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
 如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
 .
.
 .
.
 如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.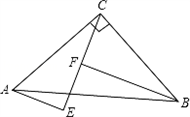
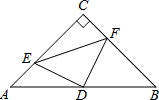

 已知:如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥CE于E,BF⊥CE于F.