设AB分别为椭圆的左右顶点(1,3|2)为椭圆上一点椭圆长半轴的长等于答案解析
科目:gzsx
来源:
题型:
(2013•闵行区二模)设双曲线x
2-y
2=6的左右顶点分别为A
1、A
2,P为双曲线右支上一点,且位于第一象限,直线PA
1、PA
2的斜率分别为k
1、k
2,则k
1•k
2的值为
1
1
.
查看答案和解析>>
科目:gzsx
来源:
题型:填空题
设双曲线x2-y2=6的左右顶点分别为A1、A2,P为双曲线右支上一点,且位于第一象限,直线PA1、PA2的斜率分别为k1、k2,则k1•k2的值为________.
查看答案和解析>>
科目:gzsx
来源:
题型:
设直线l的方程为(m2-2m-3)x+(2m2+m-1)y=2m-6,根据下列条件分别确定m的值.
(1)l在x轴上的截距是-3;
(2)l的斜率是-1.
查看答案和解析>>
科目:gzsx
来源:
题型:013
三角形的一个顶点是(1,2),两条高所在的直线方程为x+y=0和2x-3y+1=0,则第三边所在的直线方程 [ ]
A.2x-3y+7=0 B.2x+3y+7=0
C.2x+3y-7=0 D.2x-3y-7=0
查看答案和解析>>
科目:gzsx
来源:
题型:单选题
三角形的一个顶点是(1,2),两条高所在的直线方程为x+y=0和2x-3y+1=0,则第三边所在的直线方程
- A.
2x-3y+7=0
- B.
2x+3y+7=0
- C.
2x+3y-7=0
- D.
2x-3y-7=0
查看答案和解析>>
科目:gzsx
来源:
题型:
半径为
12cm的轮子,每3分钟转1 000圈,试求:
(1)它的平均角速度(1秒钟转过的弧度数);
(2)轮沿上一点1秒经过的距离;
(3)轮沿上一点转过1 000°所经过的距离.
查看答案和解析>>
科目:gzsx
来源:
题型:
半径为
12 cm的轮子,每3分钟转1 000圈.试求:
(1)它的平均角速度(1秒钟转过的弧度数);
(2)轮沿上一点1秒经过的距离;
(3)轮沿上一点转过1 000°所经过的距离.
查看答案和解析>>
科目:gzsx
来源:
题型:
判断下列命题:
①对任意两个事件A、B都有P(A·B)=P(A)·P(B);
②如果事件A发生,事件B一定发生,则P(A·B)=P(B);
③已知在一次试验中P(A)=0.1,那么在3次独立重复试验中A恰好发生2次的概率是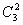 ·(0.1) 3-2·(0.9)2=3×0.1×0.81=0.243;
·(0.1) 3-2·(0.9)2=3×0.1×0.81=0.243;
④抛掷一枚硬币100次,则正面向上出现的次数超过40次.
请把正确命题的序号填在横线上:_______________.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•天津)设椭圆
+=1(a>b>0)的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
(1)若直线AP与BP的斜率之积为
-,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|>
.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2013•潮州二模)设椭圆
+=1(a>b>0)的左右顶点分别为A(-2,0),B(2,0),离心率e=
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且|QP|=|PC|.
(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线AC(C点不同于A,B)与直线x=2交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
查看答案和解析>>
科目:gzsx
来源:
题型:
设A,B分别为椭圆
+=1(a>b>0)的左右顶点,椭圆长半轴的长等于焦距,且直线x=4是它的右准线.
(Ⅰ)求椭圆的方程;
(Ⅱ)设P为椭圆右准线上不同于点(4,0)的任意一点,若直线BP于椭圆相交于两点B,N,求证:∠NAP为锐角.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•辽宁)如图,已知椭圆C
0:
+=1(a>b>0,a,b为常数),动圆C
1:
x2+y2=,b<t1<a.点A
1,A
2分别为C
0的左右顶点,C
1与C
0相交于A,B,C,D四点.
(I)求直线AA
1与直线A
2B交点M的轨迹方程;
(II)设动圆C
2:
x2+y2=与C0相交于A',B',C',D'四点,其中b<t
2<a,t
1≠t
2.若矩形ABCD与矩形A'B'C'D'的面积相等,证明:
+为定值.
查看答案和解析>>
科目:gzsx
来源:
题型:
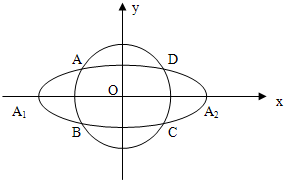
(A题)如图,在椭圆
+
=1(a>0)中,F
1,F
2分别是椭圆的左右焦点,B,D分别为椭圆的左右顶点,A为椭圆在第一象限内弧上的任意一点,直线AF
1交y轴于点E,且点F
1,F
2三等分线段BD.
(1)若四边形EBCF
2为平行四边形,求点C的坐标;
(2)设m=
,n=
,求m+n的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
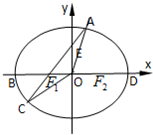
已知椭圆C:
+=1(a>b>0)的离心率为
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线 x
+y+=0相切.A、B是椭圆的左右顶点,直线l 过B点且与x轴垂直,如图.
(I)求椭圆的标准方程;
(II)设G是椭圆上异于A、B的任意一点,GH丄x轴,H为垂足,延长HG到点Q 使得HG=GQ,连接AQ并延长交直线l于点M,点N为MB的中点,判定直线QN与以AB为直径的圆O的位置关系,并证明你的结论.
查看答案和解析>>
科目:gzsx
来源:
题型:
在平面直角坐标系xoy中,已知椭圆
E:+=1(a>b>0)的离心率为
,且过点
(,).
(1)求椭圆E的标准方程;
(2)设椭圆E的左右顶点分别为A
1,A
2,上顶点为B,圆C与以线段OA
2为直径的圆关于直线A
1B对称,
①求圆C的标准方程;
②设点P是圆C上的动点,求△PA
1B的面积的最大值.
查看答案和解析>>
科目:gzsx
来源:
题型:
椭圆
+=1(a>b>0)上任一点P到两个焦点的距离的和为6,焦距为
4,A,B分别是椭圆的左右顶点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若P与A,B均不重合,设直线PA与PB的斜率分别为k
1,k
2,证明:k
1•k
2为定值;
(Ⅲ)设C(x,y)(0<x<a)为椭圆上一动点,D为C关于y轴的对称点,四边形ABCD的面积为S(x),设
f(x)=,求函数f(x)的最大值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江西南昌市高三第二次模拟测试理科数学试卷(解析版)
题型:解答题
查看答案和解析>>
科目:gzsx
来源:2010年高考试题分项版理科数学之专题二函数
题型:解答题
(16分)在平面直角坐标系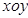 中,如图,已知椭圆
中,如图,已知椭圆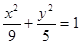 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T( )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M ,
,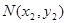 ,其中m>0,
,其中m>0,

①设动点P满足 ,求点P的轨迹
,求点P的轨迹
②设 ,求点T的坐标
,求点T的坐标
③设 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点
(其坐标与m无关)
查看答案和解析>>
科目:gzsx
来源:2010年高考试题分项版理科数学之专题三数列
题型:解答题
(16分)在平面直角坐标系 中,如图,已知椭圆
中,如图,已知椭圆 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T( )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M ,
, ,其中m>0,
,其中m>0,

①设动点P满足 ,求点P的轨迹
,求点P的轨迹
②设 ,求点T的坐标
,求点T的坐标
③设 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点
(其坐标与m无关)
查看答案和解析>>

![]() ·(0.1) 3-2·(0.9)2=3×0.1×0.81=0.243;
·(0.1) 3-2·(0.9)2=3×0.1×0.81=0.243; (2012•辽宁)如图,已知椭圆C0:
(2012•辽宁)如图,已知椭圆C0: (A题)如图,在椭圆
(A题)如图,在椭圆 已知椭圆C:
已知椭圆C: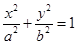 的离心率等于
的离心率等于 ,点P
,点P 在椭圆上。
在椭圆上。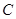 的方程;
的方程;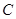 的左右顶点分别为
的左右顶点分别为 ,过点
,过点 的动直线
的动直线 与椭圆
与椭圆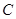 相交于
相交于 两点,是否存在定直线
两点,是否存在定直线 :
: ,使得
,使得 与
与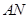 的交点
的交点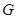 总在直线
总在直线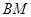 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的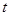 值;若不存在,说明理由.
值;若不存在,说明理由.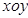 中,如图,已知椭圆
中,如图,已知椭圆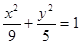 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T( )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M ,
,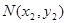 ,其中m>0,
,其中m>0,

 ,求点P的轨迹
,求点P的轨迹 ,求点T的坐标
,求点T的坐标 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点 中,如图,已知椭圆
中,如图,已知椭圆 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T( )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M ,
, ,其中m>0,
,其中m>0,

 ,求点P的轨迹
,求点P的轨迹 ,求点T的坐标
,求点T的坐标 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点