请你画出将○A先向上平移6个单位,在向左平移8个单位答案解析
科目:czsx
来源:同步轻松练习 九年级数学下
题型:044
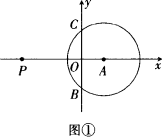
如图①,在平面直角坐标系中,以A(3,0)为圆心的⊙A被y轴截得的弦长BC=8,点P的坐标为(-8,0);
(1)求⊙A的半径;
(2)请你画出将⊙A先向上平移6个单位,再向左平移8个单位得到的⊙D.并说明⊙D与两条坐标轴及⊙A的位置关系;
(3)画出以点P为位似中心,将⊙D缩小为原来的一半的⊙E,写出点E的坐标.

查看答案和解析>>
科目:czsx
来源:
题型:
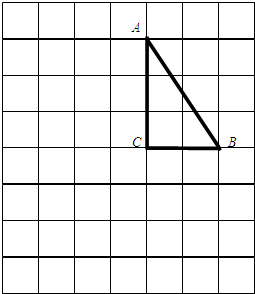
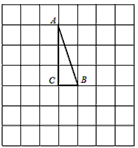
在下图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.
(1)请你画出将Rt△ABC绕点C顺时针旋转180°后所得到的Rt△A'B'C,其中A、B的对应点分别是A'、B'(不必写画法);
(2)连接AB'、A'B.若每个小正方格的边长为1,求四边形AB'A'B的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
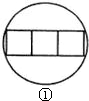
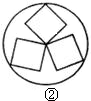
在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
cm;
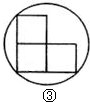
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
查看答案和解析>>
科目:czsx
来源:
题型:
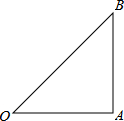
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(1)请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA
1B
1;
(2)线段OA
1的长度是
6
6
,∠AOB
1的度数是
135°
135°
;
(3)连接AA
1,求证:四边形OAA
1B
1是平行四边形.
查看答案和解析>>
科目:czsx
来源:
题型:
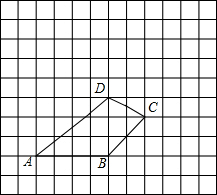
如图,四边形ABCD.
(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系,并写出点A、B、C、D的坐标.
(2)求出四边形ABCD的面积.
(3)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形A′B′C′D′.
查看答案和解析>>
科目:czsx
来源:
题型:
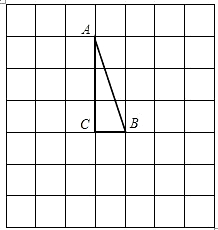
在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°
(1)请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△A′B′C′,其中A、B的对应点分别是A′、B′(不必写画法);
(2)设(1)中AB的延长线与A′B′相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).
查看答案和解析>>
科目:czsx
来源:
题型:
(本题9分)如图,四边形ABCD.
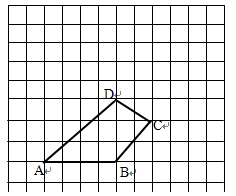
(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系,并写出点A、B、C、D的坐标。
(2)求出四边形ABCD的面积。
(3)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形

查看答案和解析>>
科目:czsx
来源:2014届广西南宁市七年级下学期第一次月考数学卷
题型:解答题
(本题9分)如图,四边形ABCD.
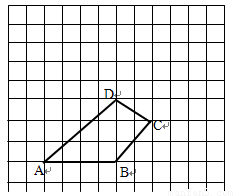
(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系,并写出点A、B、C、D的坐标。
(2)求出四边形ABCD的面积。
(3)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形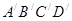
查看答案和解析>>
科目:czsx
来源:
题型:
(本题9分)如图,四边形ABCD.

(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系,并写出点A、B、C、D的坐标。
(2)求出四边形ABCD的面积。
(3)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形
查看答案和解析>>
科目:czsx
来源:2006年福建省泉州市中考数学试卷(解析版)
题型:解答题
(2006•泉州)在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°
(1)请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△A′B′C′,其中A、B的对应点分别是A′、B′(不必写画法);
(2)设(1)中AB的延长线与A′B′相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).

查看答案和解析>>
科目:czsx
来源:2009年陕西省西安市师大附中中考数学模拟试卷(杨丽敏)(解析版)
题型:解答题
(2006•泉州)在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°
(1)请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△A′B′C′,其中A、B的对应点分别是A′、B′(不必写画法);
(2)设(1)中AB的延长线与A′B′相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).

查看答案和解析>>
科目:czsx
来源:
题型:解答题
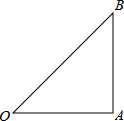 如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(1)请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1;
(2)线段OA1的长度是______,∠AOB1的度数是______;
(3)连接AA1,求证:四边形OAA1B1是平行四边形.
查看答案和解析>>
科目:czsx
来源:江苏模拟题
题型:解答题
在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示
(1)通过计算(结果保留根号与π),
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为 ______ cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为 _______ cm;
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为 _______ cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
查看答案和解析>>
科目:czsx
来源:第24章《图形的相似》中考题集(20):24.3 相似三角形(解析版)
题型:解答题
在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°
(1)请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△A′B′C′,其中A、B的对应点分别是A′、B′(不必写画法);
(2)设(1)中AB的延长线与A′B′相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).

查看答案和解析>>
科目:czsx
来源:2006年福建省泉州市初中毕业、升学考试数学试题
题型:044
查看答案和解析>>
科目:czsx
来源:第26章《圆》中考题集(12):26.1 旋转(解析版)
题型:解答题
在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°
(1)请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△A′B′C′,其中A、B的对应点分别是A′、B′(不必写画法);
(2)设(1)中AB的延长线与A′B′相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).

查看答案和解析>>
科目:czsx
来源:
题型:解答题
 在下图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.
在下图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.
(1)请你画出将Rt△ABC绕点C顺时针旋转180°后所得到的Rt△A'B'C,其中A、B的对应点分别是A'、B'(不必写画法);
(2)连接AB'、A'B.若每个小正方格的边长为1,求四边形AB'A'B的面积.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
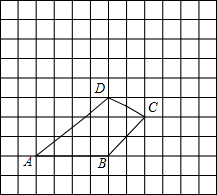 如图,四边形ABCD.
如图,四边形ABCD.
(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系,并写出点A、B、C、D的坐标.
(2)求出四边形ABCD的面积.
(3)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形A′B′C′D′.
查看答案和解析>>
科目:czsx
来源:
题型:044
在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°
⑴请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△ ,其中A、B的对应点分别是
,其中A、B的对应点分别是 、
、 (不必写画法);
(不必写画法);
⑵设⑴中AB的延长线与 相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1)
相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1)

.
查看答案和解析>>
科目:czsx
来源:福建省中考真题
题型:解答题
在下图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°。
(1)请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△A′B′C′,其中A、B的对应点分别是A′、B′(不必写画法);
(2)设(1)中AB的延长线与A′B′相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1)。
查看答案和解析>>



 在下图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.
在下图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.


 (2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6. 如图,四边形ABCD.
如图,四边形ABCD. 在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°
在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°



![]()


 如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
如图在Rt△OAB中,∠OAB=90°,OA=AB=6.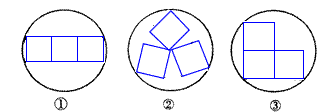


![]() ,其中A、B的对应点分别是
,其中A、B的对应点分别是![]() 、
、![]() (不必写画法);
(不必写画法);![]() 相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).
相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).

 在下图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.
在下图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°. 如图,四边形ABCD.
如图,四边形ABCD.![]() ,其中A、B的对应点分别是
,其中A、B的对应点分别是![]() 、
、![]() (不必写画法);
(不必写画法); ![]() 相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1)
相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1)